Александр Волошинов - Математика и искусство

Но закончить разговор о пропорциях церкви Вознесения в Коломенском нам хочется словами автора математического анализа ее пропорций, Шевелева. "Подчеркнем выразительнейшую деталь размерной структуры, наиболее ярко показывающую особенность логики древнего мастера, стремящегося особенно точно выразить в метрологии главное. Так же как 10 саженей определили, по существу, весь храм, его ядро, так же и 10 локтей определили символ и венчание церкви — крест (10С тХ10С тХ10С т— четверик; 10С тХ10С тХ10К н— призма четверика; 10Л тХ10Л т— соразмерность креста, ибо в нем заключен для зодчего и смысловой символ соединения, и символ торжества вертикали, и символ храма, и символ пропорции, построившей этот образ)".

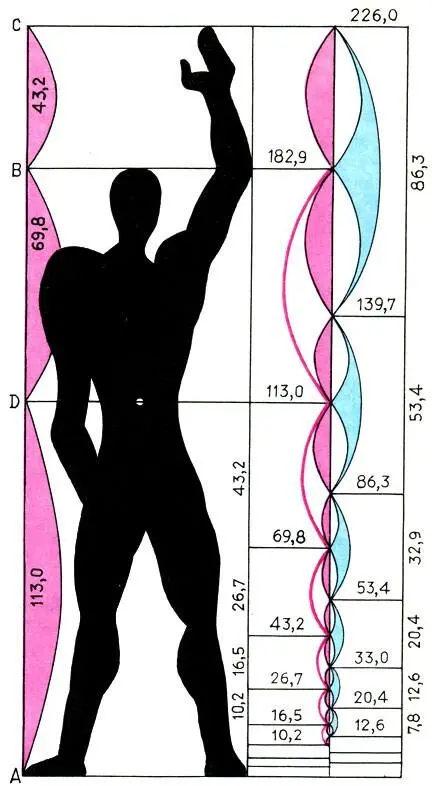
Модулор Ле Корбюзье. Рисунок Ле Корбюзье. 'Модулор — это измерительный прибор, в основе которого лежат человеческий рост и математика' (Ле Корбюзье)

Нам остается только добавить, что село Коломенское давно уже стало частью современной Москвы и тем, кто не знает этого, мы рекомендуем сойти на одноименной станции метро и воочию убедиться в гениальности безвестных русских мастеров. Ну а те, кто знаком с храмом Вознесения, быть может, захотят теперь взглянуть на него другими глазами, увидеть в нем не только причудливую игру воображения художника, но и мудрый расчет изощренного ума мастера.

Коль скоро речь у нас зашла о метро, то перенесемся, наконец, в современный XX век. Время поисков пропорций и сегодня не кануло в Лету, напротив, по мнению Ле Корбюзье, оно только настало.

Мы уже отмечали (с. 220), что антропометрические меры благодаря своему происхождению оказались как нельзя лучше приспособлены для конструирования архитектурной среды. Мы только что убедились в том, что антропометрические меры содержали в себе замечательные пропорции, позволявшие древним мастерам создавать прекрасные памятники архитектуры.

7 апреля 1795 г. во Франции была введена метрическая система мер, в разработке которой участвовали такие крупнейшие ученые, как Лаплас, Монж, Кондорсе. За единицу длины — метр — была принята 1/10 000 000 часть 1/4 длины парижского географического меридиана. Метрическая система обладала бесспорными преимуществами и все шире раздвигала границы своего существования. Однако метр никоим образом не был связан с человеком, и, по мнению Ле Корбюзье, для архитектуре это имело самые серьезные последствия^ "Принимая участие в постройке хижин, жилых домов, храмов, предназначенных для потребностей человека, метр, по-видимому, ввел в них чужие и чуждые единицы измерения и, если мы присмотримся к нему ближе, может быть обвинен в дезориентации современной архитектуры и ее искажении... Архитектура, построенная на метрических измерениях, сбилась с правильного пути".

Но главная причина, толкавшая зодчих XX века на поиски новых систем измерений в архитектуре, была все-таки не в недостатках метрической системы мер. Английская архитектура с постоянством продолжала пользоваться футами и дюймами, но и у нее возникли те же проблемы. Дело было в том, что вместе с XX веком в архитектуру пришли невиданные объемы и темпы строительства. Проектирование архитектурной среды стало преимущественно типовым, а сама архитектура — индустриальной. В этих условиях строительные элементы необходимо было стандартизировать и унифицировать. Кроме того, архитекторам хотелось бы примирить непримиримое: красоту и стандарт. Требовалось найти такие методы пропорционирования, которые обладали бы максимальной гибкостью, простотой и универсальностью. "Если бы появился какой-нибудь линейный измеритель, подобный системам музыкальной записи, не облегчился бы ряд проблем, связанных со строительством?" — спрашивал Ле Корбюзье. И в 1949 г. он сам отвечает на этот вопрос, предложив в качестве такого измерителя систему модульной унификации — модулор.

Идея построения модулора гениально проста. Модулор — это ряд золотого сечения (15.2):

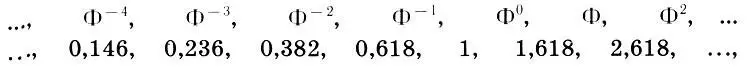(17.1)

умноженный на два коэффициента. Первый коэффициент k 1равен росту человека; умножая (17.1) на k 1, Корбюзье получает так называемый красный ряд. Второй коэффициент k 2равен расстоянию от земли до конца поднятой руки человека (это большая сажень в древнерусской системе мер)- При умножении (17.1) на k 2получается синий ряд. Осталось только выбрать числовые значения коэффициентов. Желая примирить в моду лоре английскую и французскую системы мер, а также следуя античной традиции, согласно которой рост человека равен 6 футам, Корбюзье взял в качестве k 16 английских футов, т. е. k 1= 6*30,48 = 182,88 см. Значение k 2принято равным 226,0 см. Так были получены красный ряд:

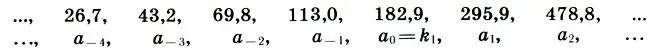(17.2)

и синий ряд:

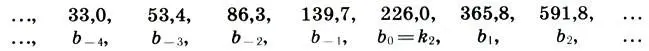(17.3)

Значение k 2было выбрано еще и так, чтобы между красным и синим рядами существовала простая связь:

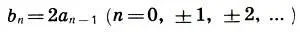(17.4)

Следовательно, синий ряд фактически есть удвоение красного ряда.

Будучи геометрическими прогрессиями, члены обоих рядов модулора образуют цепь равных отношений: a n+1:a n= b n+1:b n= Φ, т. е. в моду лоре воплощается принцип гармонии: "из всего — единое, из единого — все". Благодаря аддитивному свойству золотого сечения "части" модулора сходятся в "целое". Наконец, абсолютные значения шкал модулора происходят от человека и потому хорошо приспособлены для проектирования архитектурной среды. Так, по мнению автора, модулор вносит порядок, стандарт в производство и в то же время связывает все его элементы законами гармонии.

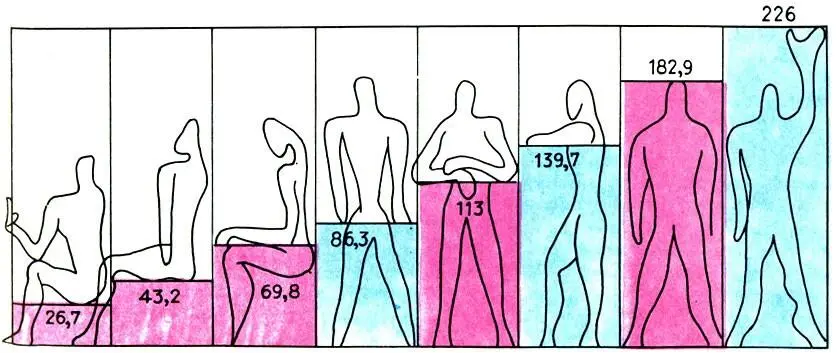
Числа красной и синей шкал модулора — действительные размеры, соответствующие определенным положениям тела человека. Рисунок Ле Корбюзье

Капелла в Роншане. 1958 (б). Эти два антипода в творчестве великого зодчего, две различные философии в архитектуре связаны воедино гаммой архитектурных пропорций — модулором