Александр Волошинов - Математика и искусство

Церковь Покрова была построена в 1165 г. А через 73 года она стала свидетельницей небывалой в истории России беды: полчища Батыя, превратив в пепелище Рязань, Коломну и Москву, осадили Владимир. Русскому государству, истерзанному княжескими раздорами, был нанесен смертельный удар, оправиться от которого в полной мере Россия смогла только через 200 лет, к концу XV века.

Церковь Вознесения в селе Коломенском (ныне Москва). 1532. Шедевр древнерусского зодчества, один из первых каменных шатровых храмов на Руси

В 1530 г. в царской усадьбе — селе Коломенском под Москвой — родился будущий царь пробуждающейся России Иван Грозный. А через два года здесь же, в Коломенском, на крутом берегу Москвы-реки, было завершено строительство церкви, поставленной в память об этом событии. Зодчие будто предвидели рождение небывало грозного царя: церковь тоже была небывалой. В ней все", и высота (почти 62 м), и каменный шатер, и устремленная ввысь форма — было невиданным. Новый храм словно символизировал прорыв России в свободное от татарского ига будущее. "...Бе же церковь та велми чюдна высотою и красотою и светлостию, такова не бывала прежде на Руси",- писал о ней летописец. Весь пропорциональный строй церкви, все ее безудержное стремление ввысь как нельзя более соответствовали названию — храм Вознесения.

Но для нас храм Вознесения интересен еще и тем, что он является не только гимном расправляющей крылья России, но и архитектурным гимном геометрии.

Ни один из рассмотренных архитектурных шедевров, в том числе и Парфенон, не настолько пронизан геометрией, не настолько прост и лаконичен в своей размерной структуре, как храм Вознесения в Коломенском. Соразмерности храма с предельной ясностью определены двумя парными мерами: горизонтальные — малой (тмутараканской) саженью С ти косой новгородской саженью К н(С т:К н= 1:√2), вертикальные — малой саженью С ти мерной саженью С м(С т:С м= 1:(√5 — 1)) и их комбинацией С м:2С т= (√5 — 1):2 = φ, дающей золотое сечение. Таким образом, храм Вознесения является также прекрасным примером применения московскими мастерами измерительного инструмента типа новгородской мерной трости, созданной, как мы помним, для работы именно этими двумя парами мер (см. с. 220). Рассмотрим пропорциональ-ный анализ храма, сделанный архитектором Шевелевым.

В основу плана церкви Вознесения положен квадрат ABCD со стороной в 10 малых сажень: а = АВ = 10С т. Ясно, что диагонали квадрата равны 10 косым новгородским саженям: AC = BD = 10√2СТ = 10К н. Так с помощью парных мер С ти К носуществлялся контроль правильности построения исходного квадрата. Окружность радиуса R = 5K н, описывающая квадрат, определяет положение всех 12 наружных углов плана храма. Вписав через середины сторон в квадрат ABCD новый квадрат и сделав построения, мы получим внешний контур плана — 20- уголъник . Выступающие над исходным квадратом части называются притворами, их ширина равна а/2 = 5С т. Выразив радиус описанной окружности R в мерных саженях и отложив эту величину в малых саженях, строители получали сторону квадрата b, определяющего внутреннее пространство храма:

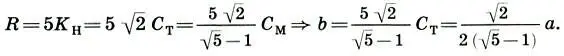
Разумеется, коломенские мастера не вычисляли никаких радикалов! Они просто прикладывали мерную трость разными сторонами и автоматически переходили из одной меры в другую. План церкви построен. А мы выразим еще сторону квадрата с, охватывающего притворы: с = √7/ 2а (треугольник, из которого находится с/2, на чертеже не показан, чтобы не портить красоту центральной симметрии плана; найдите его). Зная а, b, с, легко выразить все остальные размеры плана и соотношения между ними.

Перейдем к объемам и вертикальным членениям храма. Церковь Вознесения со всех сторон окружена крытой галереей, поднятой над уровнем земли и называемой гульбищем . Гульбище делалось на уровне перекрытия подклета — полуподвального помещения, используемого в хозяйственных целях. Вход в церковь устраивался с гульбища, на которое в храме Вознесения ведут три крыльца, и, таким образом, вертикальные размеры церкви с гульбищем воспринимаются от уровня последнего.

Основной объем храма составляет 20-гранная призма, поставленная на подклет. Ее высота равна стороне исходного квадрата а. Таким образом, ядром основного объема является куб — четверик а×а×а (а=10С т), украшенный гранями притворов. Вместе с подклетом высота 20-гранной призмы равна диагонали исходного квадрата а√2 = 10√2С т= 10К н. Итак, сторона и диагональ исходного квадрата (ядра плана) полностью определяют вертикальные размеры основного объема (ядра основания).

Двадцатигранная призма основного объема через затейливый пояс кокошников переходит в восьмигранную призму — восьмерик . Восьмерик также вписан к куб d×d×d(d = 9C т). Затем восьмерик переходит в восьмигранный шатер, высота которого h = d√2 = 9√2С т= 9К н, т. е. шатер вписан в прямоугольный параллелепипед 9С т×9С т×9К н. Площадь верхнего сечения шатра уменьшена в 16 раз, а его линейные размеры — в 4 раза. Поскольку 1/4 сажени равна локтю, то, следовательно, верхнее сечение вписано в квадрат где Л т— малый (тмутараканский) локоть (4Л т= С т). Наконец, через венчающий карниз шатер завершается восьмигранным барабаном, сечение которого на малый полулокоть превышает верхнее сечение шатра. Барабан чуть нависает над шатром и вписан в куб f×f×f (f = 9,5Л т), а вместе с главкой, взятой без яблока (см. рис. на с. 242), барабан вписан в прямоугольный параллелепипед f×f×√2f.

Итак, мы видим как сторона ядра плана а, измеренная то малой саженью, то косой новгородской, рождает все главные вертикали храма. Заметим, что общая высота церкви от верха цоколя до яблока, на котором стоит крест, равна 4а = 40С т, т. е. также простейшим образом выражается через исходный размер а. И еще одно важное отношение. Пояс кокошников, через который четверик основания переходит восьмерик шатра, делит храм на две части — основание и завершение. Высота основания h 1≈14C т, а высота завершения h 2≈14K н, откуда h 1:h 2= C т:K н= 1:√2, т. е. главные вертикальные членения храма также относятся как малая и косая новгородская сажени.

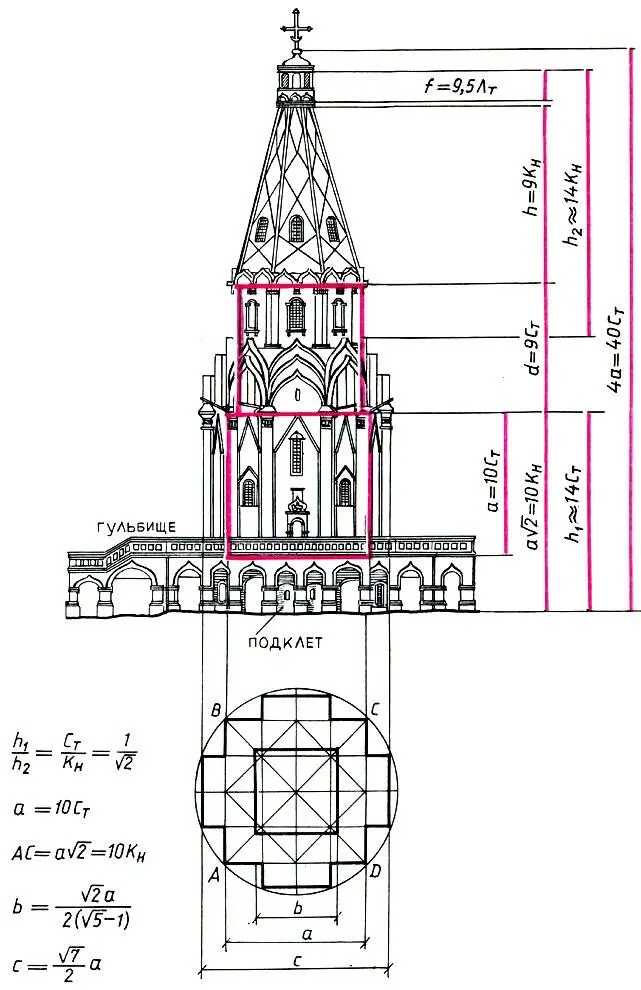
Пропорциональный строй церкви Вознесения в Коломенском (по Шевелеву)

Но пропорции храма Вознесения определены не одной, а двумя математическими закономерностями. Помимо пропорции С т:К н= 1:√2, определяющей основание, статическое начало храма, есть в нем и другая тема — тема развития вверх, вознесения, которая определена пропорциональной цепью: С т:С м= 1:(√5 — 1), а также пропорцией золотого сечения: С м:2С т=φ. В проведении этой темы соблюден знакомый нам по Парфенону принцип встречного движения пропорций. Две разные пропорциональные цепи накладываются друг на друга, сталкиваются и противоборствуют. В этом столкновении двух противоборствующих начал — горизонтального и вертикального — и заключается архитектурный образ церкви Вознесения. Не останавливаясь на математическом анализе этих двух систем, предоставим слово автору прекрасного эстетического анализа церкви Вознесения, искусствоведу А. Циресу. "В образе этой церкви,- пишет Цирес,- сплетаются два основных лейтмотива: мотив острого, полного столкновений и диссонансов динамизма и мотив гармонически спокойной красоты... Сложный ритм арок нижних галерей... идет, учащаясь от краев к центру,... теснит арки от краев к углам основного массива церкви и к ее середине,... подсказывает смену горизонтального движения движением, направленным ввысь... Так снизу вверх идет последовательное смягчение кристаллизма и нарастание компактности объема, вплоть до его стянутости в крепкий узел, венчающий всю объемную композицию главкой".