Александр Волошинов - Математика и искусство

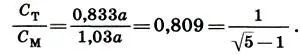(17.1)

Следовательно, малая сажень С тотносится к мерной С мкак сторона двойного квадрата к его диагонали без малой стороны:

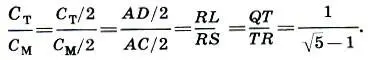
Из (17.1) ясно, что отношение мерной полусажени С м/2 к малой сажени С травно золотому сечению:

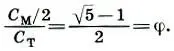(17.2)

Итак, в установленном самой природой отношении полуразмаха рук (RS) к высоте туловища (LQ), т. е. в отношении двух основных мер Древней Руси, заключено золотое сечение, столь распространенное в древнерусской архитектуре.

Рост человека: а = АВ

Мерная сажень: С н= AC = CN = 1,03a

Малая (тмутараканская) сажень: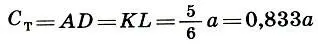

Сажень без чети: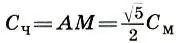

Косая новгородская сажень :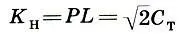

Косая великая сажень: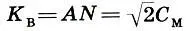

Соотношения между саженями: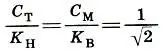

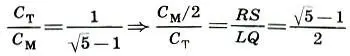
— золотое сечение

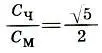
— функция золотого сечения

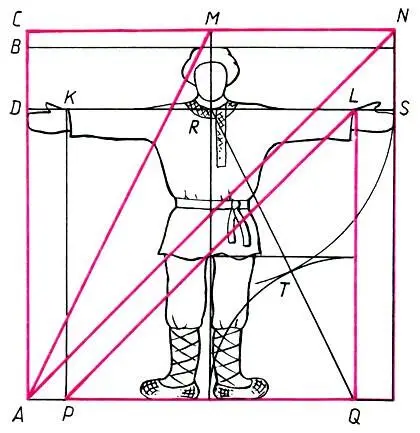
Основные древнерусские меры длины и геометрическая взаимосвязь между ними

Построив квадраты на малой С ти мерной С мсаженях и проведя в них диагонали, мы получаем еще два типа саженей: косую новгородскую сажень 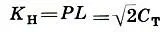и великую косую сажень 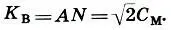. В отличие от первых двух саженей (малой и мерной), выражающих природные меры, косые сажени получены чисто геометрическим путем. Ясно, что

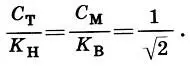(17.3)

Наконец, существовала еще одна сажень, получаемая геометрическим путем. Это так называемая сажень без чети С ч, равная диагонали AM половины квадрата, построенного на мерной сажени С м. У этой сажени не было соответствующей косой пары, и поэтому ее называли саженью без пары, без четы, или без чети. Из треугольника АСМ следует, что 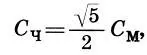, откуда

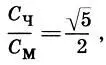(17.4)

т. е. отношение сажени без чети С чк мерной сажени С мравно функции золотого сечения (см. с. 219).

Таковы лишь основные типы саженей, существовавших в древнерусской метрологии. Новгородская мерная трость, найденная в 1970 г. (см. с. 219), позволила уточнить их размеры. Новгородские меры XII века соответствуют росту человека: а = 170,5 см. Тогда С м= 175,6 см, С т= 142,1 см, К н= 200,9 см, К в= 248,3 см, С ч= 196,3 см. Если же рост человека принять равным 6 греческим футам: а = 6*30,87 = 185,22 см, то для основных саженей (мерной и малой) получим значения: С м= 190,8 см и С т= 154,3 см. Именно эти меры наиболее часто встречаются в древнерусских храмах XI века, строительство которых, по-видимому, велось византийскими мастерами. Так, вместе с христианством Русь наследовала византийскую систему мер, которая в свою очередь взросла на античной средиземноморской культуре. Абсолютные размеры саженей в России с течением времени сильно колебались вплоть до введения метрической системы мер в 1918 г. Но важно то, что пропорциональные отношения между парными саженями сохранялись. Эти пропорции становились пропорциями архитектурных сооружений.

О том, что меры древнерусскими строителями применялись парами, свидетельствует, например, новгородская грамота XVI века, которая так описывает размеры Софийского храма в Новгороде: "а внутри главы, где окна,- 12 сажен, а от Спасова образа ото лбу до моста церковного — 15 сажен мерных". (Обмеры показывают, что упоминаемые сажени соотносятся как 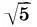:2.) О применении парных мер говорит и новгородская мерная трость, в которой малая сажень С тиспользовалась либо в паре с мерной саженью С м(С т:С м= 1:( 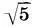— 1)), либо с косой новгородской К н(С т:К н= 1:√2). Если же на новгородской трости брались мерные полусажени в паре с малой саженью, то эта пара давала золотое сечение (С м/2:С т=φ). Итак, красота пропорций древнерусской архитектуры заложена в самой системе древнерусских мер, дающей такие важнейшие пропорции, как золотое сечение, функция золотого сечения, отношение двойного квадрата.

Но помимо всех этих пропорций, которые от самой природы перешли в систему мер, а затем и в архитектурные памятники, был у древнерусских мастеров и еще один секрет. Именно этот секрет позволял придавать каждому древнему сооружению неповторимую прелесть, "нюанс", как говорят архитекторы. Секрет этот раскрыт в рядной записи плотника Федора на постройку деревянной церкви Усть-Кулуйского погоста (кон. XVII в.), где сказано: "А рубить мне, Федору, в высоту до порога 9 рядов, а от полу до поволоки — как мера и красота скажет..."

" Как мера и красота скажет ..." Эта замечательная формула безвестного русского плотника выражает суть диалектики взаимодействия рационального (мера) и чувственного (красота) начал в достижении прекрасного, союз математики (мера) и искусства (красота) в создании архитектурных памятников.

Перейдем, наконец, к анализу пропорций церкви Покрова на Нерли. Этот архитектурный шедевр для русского человека значит столько же, сколько Парфенон для грека. Поэтому неудивительно, что пропорциональный строй небольшой церкви анализировался многими исследователями и каждый из них старался дать свою "окончательную" разгадку тайны ее очарования. Рассмотрим кратко и мы пропорции церкви Покрова на Нерли с двух точек зрения.