Александр Волошинов - Математика и искусство

Древние греки прекрасно знали особенности оптического восприятия человеческого глаза: строго вертикальные и параллельные колонны кажутся распадающимися, а горизонтальная балка — прогнувшейся книзу.

Но даже оптические поправки в Парфеноне подчинены закону 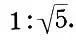Действительно, нижний диаметр угловых колонн больше "теоретического диаметра" b 2= a:5( 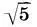+ l) = 190,79 см на 2,96 см, а у рядовых — меньше на 1,32 см. Взяв отношение этих поправок, мы с изумлением обнаруживаем: 1,32:2,96 = 0,446 ≈ 1:( = 0,447!

Оптические иллюзии восприятия. Так выглядел бы Парфенон, если бы его линии были строго горизонтальны и вертикальны (а). Таков Парфенон в действительности (б). Парфенон, каким мы его видим благодаря оптическим поправкам (в). Наклоны и искривления прямых сильно преувеличены

Раз уж мы заговорили об отличии "теоретических" размеров Парфенона от истинных, следует расставить все точки над i. Разумеется, совпадение "теоретических" размеров (см. (16.1) — (16.4) и рис. на с. 222) с реальными размерами Парфенона не является абсолютным. Относительные расхождения теории с действительностью колеблются в пределах от 05% до 1,6%. Наибольшее расхождение получается для высоты антаблемента — 3,5%. Это и понятно, ибо высота антаблемента — единственный размер в "пропорциональном дереве Парфенона", полученный не с помощью закона пропорциональности 1:( 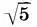, а выражением через другие размеры. Таким образом, антаблемент является наиболее слабым местом в теории Шевелева, и эта слабость теории автоматически проявилась в математической оценке погрешностей. Впрочем, как нам кажется, и такая точность в расстояниях между горизонтальными линиями сооружения (3,5 см на 1 м) является желанным эталоном для некоторых современных строителей.

Заканчивая наш анализ пропорций Парфенона, естественно поставить вопросы: является ли теория Шевелева окончательной теорией Парфенона? Таков ли на самом деле был план построения чертежа Парфенона мудрым Иктином? Ответы на эти вопросы, возможно, даст время. Ибо, как это ни парадоксально, но чем дальше мы уходим от древних, тем лучше мы их узнаем. В этом убеждает нас весь ход развития исторической науки.

И последнее. Внимательный читатель должен задать еще один вопрос: а как теория Шевелева стыкуется с "теориями золотого сечения Парфенона", рассмотренными нами в главе 14? Напомним, что там мы привели к общему знаменателю разнообразные теории пропорций Парфенона, Цейзинга, Жолтовского, Гримма, Хэмбриджа и Месселя и показали, что все они, несмотря на внешнее различие, дают золотое сечение в главных вертикалях Парфенона, т. е. в отношении несущих частей с 1к несомым с 2(см. с. 202). А как обстоит дело с этим отношением в теории Шевелева? Из рисунка ясно, что

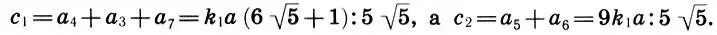
Поэтому

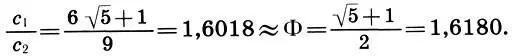(16.5)

Итак, мы выполнили обещание, данное на с. 203, и показали, что и теория Шевелева, столь не похожая на все остальные теории Парфенона, там, где оно есть, с большой точностью дает золотое сечение. Точные обмеры показывают, что в самом Парфеноне закон золотого сечения выполнен приблизительно.

(Для поклонников золотого сечения покажем, что в теории Шевелева таковое имеется и в чистом виде. Например, отношение а 1:(a 2+ a 5) = l:2k 1= ( 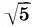+ 2):2 = Φ. Этот факт еще раз говорит только о том, что двойной квадрат 1: 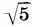тесно связан с золотым сечением.)

Прежде чем окончательно расстаться с Парфеноном, заметим, что и пропорции этого шедевра, и дорический ордер, в котором он выполнен, были не единственными архитектурными канонами, созданными гениальными древними греками. Неподалеку от Парфенона, на том же священном для древних и для современной цивилизации Акрополе, возвышается и другой бессмертный шедевр — храм Афины и Посейдона-Эрехтея — Эрехтейон, построенный чуть позже Парфенона, в 421 — 406 гг. до н. э. Но как не похоже это изящное и изысканное асимметричное сооружение, исполненное в ионическом ордере, на спокойный, строгий и симметрично уравновешенный Парфенон! Сколь отличны их пропорции! Достаточно сказать, что колонны Эрехтейона "вдвое стройнее": в них отношение диаметра основания к высоте равно 1:10. Но пропорции Эрехтейона — это еще одна увлекательная страница в архитектуре античности. А нас уже ждут гулкие своды готики.

Из светлого и жизнеобильного мира Древней Эллады перенесемся сквозь полтора тысячелетия в сумрачную эпоху европейского средневековья. Как все переменилось! Иная культура, иная философия, иная религия, иная архитектура... Вместо озаренной улыбкой античной любви к жизни и человеку — философия "умерщвления плоти", презрения земных радостей, аскетизма. Любые ростки свободной мысли, всякий вольный полет фантазии проходили через безжалостное прокрустово ложе церковных канонов. Но и в этих условиях

"В те времена каждый родившийся поэтом становился зодчим. Рассеянные в массах дарования, придавленные со всех сторон феодализмом... не видя иного исхода, кроме зодчества, открывали себе дорогу с помощью этого искусства, и их илиады выливались в форму соборов. Все прочие искусства повиновались зодчеству и подчинялись его требованиям... Архитектор — поэт — мастер в себе одном объединял скульптуру, покрывающую резьбой созданные им фасады, и живопись, расцвечивающую его витражи, и музыку, приводящую в движение колокола и гудящую в органных трубах. Даже бедная поэзия, подлинная поэзия, столь упорно прозябавшая в рукописях, вынуждена была под формой гимна или хорала заключить себя в оправу здания..." (В. Гюго. "Собор Парижской Богоматери").

Но если греческое сознание всегда было обращено к человеку, если даже в дорических колоннах греки видели торжественное могущество мужского тела, а в изящных завитках ионических волют — женскую грацию и кокетство, то ни о каких реминисценциях с пропорциями человеческого тела в готической архитектуре не могло быть и речи. Человеческая плоть презиралась христианской религией, и в пропорциях готики господствует холодная геометрия. Треугольники и квадраты — простейшие геометрические фигуры — вот основа готических пропорций; триангулирование и квадрирование [28] Триангулирование и квадрирование — методы геометрических построений, в основе которых лежат треугольники (лат. triangulum) или четырехугольники (лат. guadratus) и, в частности, квадраты. — вот методы достижения гармонии в готике. Но ведь и чистая геометрия прекрасна, и она смогла стать теоретической базой готической архитектуры, которая, по словам Гоголя, "есть явление такое, какого еще никогда не производил вкус и воображение человека".