Александр Волошинов - Математика и искусство

Мы употребили немало терминов, относящихся к классическому ордеру. Ордер (от лат. ordo — порядок) — это тип архитектурной композиции, названный так Витрувием и основанный на художественной переработке стоечно-балочной конструкции (см. с. 181). Огромную роль в развитии европейской архитектуры сыграли родившиеся в Древней Греции классические ордеры: дорический, ионический и коринфский . Название ордера происходит от названия соответствующей области Древней Греции или Малой Азии. Все последующие архитектурные стили, не говоря уже о зодчестве Возрождения и классицизма, развивались под влиянием классического ордера. Наиболее древний — дорический — ордер (ордер Парфенона) отличается торжественной монументальностью форм, строгостью пропорций и лаконизмом деталей.

Основные элементы дорического ордера, видимые на главном фасаде Парфенона, и их выражение через ширину стилобата: а = 100 фут. = 30,87 м

Итак, в дорической колонне воспроизведены пропорции несущей части мужского тела 1:5. В том же отношении находятся и крайние размеры всего Парфенона — высота колоннады и длина храма. Но вспомним Платона: "невозможно, чтобы две вещи совершенным образом соединились без третьей...", которая является их средним геометрическим (см. с. 195) [27] Хотя Платон в период строительства Парфенона еще не родился, но сохранившееся в его сочинениях учение о пропорциональности восходит к самому Пифагору и было, безусловно, известно Иктину и Калликрату — зодчим Парфенона. . Следовательно, пропорции Парфенона должны определяться еще одной величиной — средним геометрическим чисел 1 и 5, т. е. 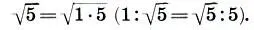Ho ведь √5 есть не что иное, как диагональ двойного квадрата! Таким образом именно парная мера 1:√5 являлся ключом к пропорциональному строению всего Парфенона! Вслед за Шевелевым нам остается только убедиться в справедливости этой гипотезы. В самом деле, между крайними размерами — высотой колоннады и длиной храма — должно лежать и их среднее геометрическое — ширина сооружения. Размеры Парфенона подтверждают это:

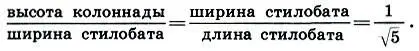(16.1)

Поскольку ширина стилобата точно равна 100 греческим футам, то естественно предположить, что именно этот размер был выбран за исходный размер Парфенона. Итак, если ширина стилобата равна а, то согласно (16.1) его длина b = a√5, a высота колоннады а 1= а:√5. Так же и шаг колонн связывает всю колоннаду в единое целое и является средним геометрическим диаметра колонны и высоты ее ствола:

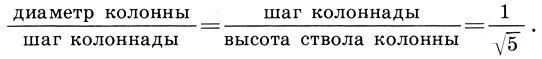(16.2)

Высота колоннады а 1складывается из высот колонны и антаблемента либо из высот нагрузки а 2и ствола колонны а 3, т. е. а 1= а 2+ а 3. Последние две высоты также относятся как 1:√5, откуда легко получить выражение а 3через а 1.

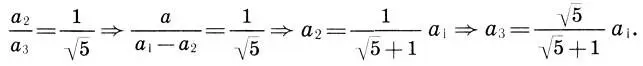
Зная высоту ствола колонны а 3, из (16.2) находим шаг колоннады b = а 3:√5 и диаметр колонны b 2= b 1:√5.

Далее. В композиции главного фасада Парфенона можно выделить две пары связанных между собой элементов. Первая пара — это два горизонтальных каменных пояса: нагрузка а 2и стереобат а 4. Эта пара связана числом членений: стереобат и нагрузка содержат по четыре элемента. (Возможно, число элементов в этих парах навеяно учением о четырех стихиях, ибо Парфенон является воплощением в камне всей античной философии.) Вторую пару образуют стволы колонн а 3и фронтон а 5. Обе пары связаны все тем же законом пропорциональности 1:√5:

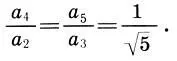(16.4)

Таким образом, "главный фасад оказался зарифмован через строку,- пишет Шевелев.- Причем движение от меньшего к большему (от стереобата к нагрузке), определенное пропорциональной связью первой пары, уравновешено движением от меньшего к большему второй пары (фронтон — ствол колонны), которое противоположно направлено".

Перейдем к оставшимся вертикальным Размерам Парфенона. Высота капители а 7и диаметр колонны b 2опять же соотносятся как 1: 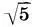, откуда а 7=b 2: 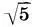= а:5 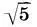( 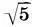+ 1). Зная а 7, легко выразить высоту антаблемента: а 6= а 2— а 7= 4а:5 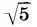( 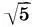+ 1). Наконец, антаблемент а 6и капитель а 7разделены одинаково, зеркально-симметрично, в отношении 1:1: 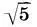на части х, х, х: 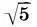и y, y, y: 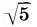соответственно. Тогда из условия x+x+x: 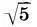= a 6и у+у+у: 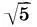= а 7находим: x = k 2a 6, y = k 2a 7, k 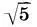2= :(2 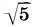+ 1), т. е. находим высоты составляющих антаблемент частей — архитрава а 8= k 2a 6, фриза а 10= k 2а 6и карниза a 12= k 2a 6: 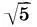, а также высоты элементов капители — абака a 9= k 2a 7, эхина a 11=k 2a 7и шейки а 13= k 2а 7: .

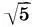Таковы лишь основные идеи пропорционального деления основных элементов Парфенона.

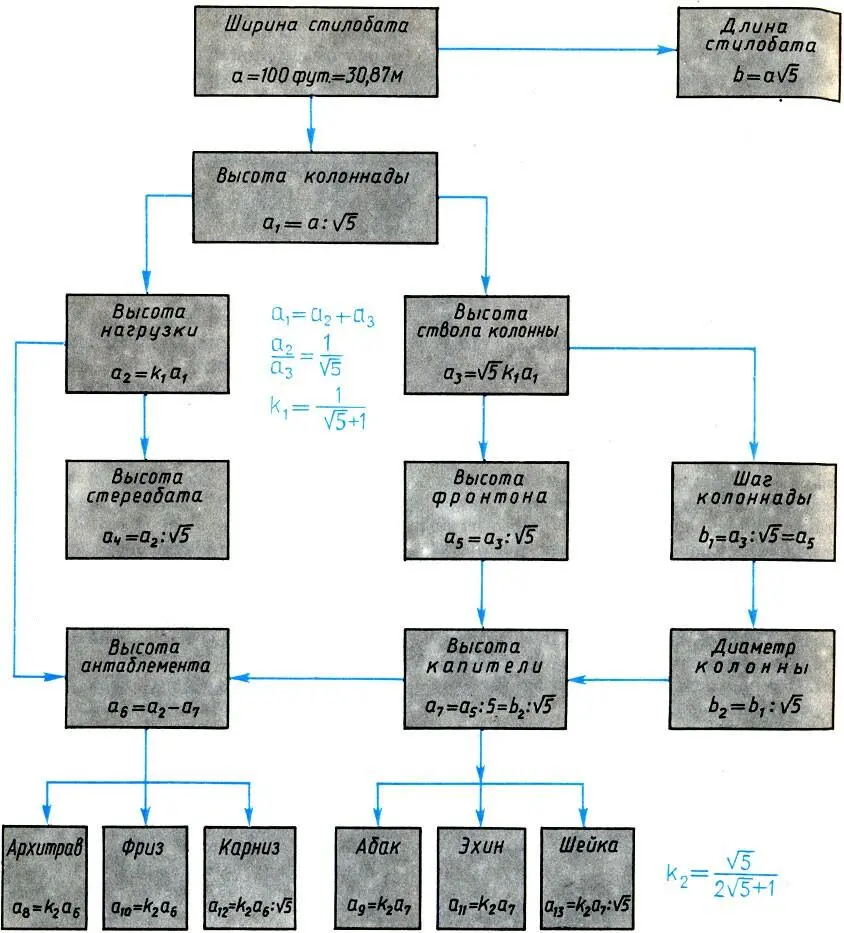
Пропорциональное дерево Парфенона (по Шевелеву). Все размеры храма от длины стилобата b = 69,5 м до высоты шейки а 13= 0,158 м выражаются через ширину стилобата: а = 100 фут. = 30,87 м

А более пытливому исследователю Парфенон открывает и свои более сокровенные тайны. Оказывается, что угловые колонны в Парфеноне толще остальных, рядовых, и сближены с ними. Отношение верхнего диаметра к нижнему в угловых колоннах менее контрастно, чем в рядовых. Такая расстановка колонн логична: ведь и в жизни сильных людей ставят на флангах. Но дело не столько в этом. Дело в том, что угловые колонны смотрятся на фоне яркого неба Эллады. Солнечные лучи дифрагируют, огибают угловые колонны. Поэтому если их сделать одинаковыми с рядовыми колоннами, которые смотрятся на темном фоне целлы — святилища храма, то угловые колонны будут казаться тоньше. Итак, в конструкцию Парфенона введены так называемые оптические поправки.