Александр Волошинов - Математика и искусство

Боттичелли. Рождение Венеры. Ок. 1483-1484. Нет живописи более поэтичной, чем живопись Боттичелли, и нет у великого Сандро картины более знаменитой, чем его 'Венера'. Неповторимо нервное изящество боттичеллиевских линий и болезненная хрупкость его вытянутых фигур. Неповторима младенческая чистота Венеры и кроткая печаль ее взора. Неповторим льнущий к телу клубок золотых волос Венеры, в котором, как в клубке змей, таится роковое коварство этого безгрешного существа. Но для неоплатоника Боттичелли его Венера, так же как и для неопифагорейца Поликлета его Дорифор,- это воплощение идеи универсальной гармонии золотого сечения, господствующего в природе

Пропорциональный анализ Венеры убеждает нас в этом

Итак, ряд золотого сечения (15.4), (15.5) и тесно связанный с ним ряд Фибоначчи (15.6) обладают массой исключительных математических свойств, которые каким-то поразительным образом сошлись в этих феноменах. Но золотое сечение и числа Фибоначчи имеют не менее удивительные приложения не только в искусстве (с чем мы немного познакомились в гл. 4 и гл. 12), но и в живой природе. К настоящему времени накоплено множество фактов, показывающих, что ряд Фибоначчи проявляется в формах живой природы как закон единообразного роста. Ряд Фибоначчи обнаружен и в расположении семян подсолнечника или сосновой шишки, и в распределении листьев и хвои на деревьях, и в расположении стеблей. Возьмите линейку и измерьте длину трех фаланг среднего пальца и пясти. Поделив эти числа на длину первой фаланги, вы с поразительной точностью обнаружите 4 члена ряда золотого сечения (15.4):

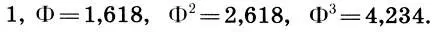
Но самым удивительным, пожалуй, является то, что точка, питающая новую жизнь,- пуп человека — делит тело человека в золотом сечении.

Что стоит за этими и многими другими фактами — игра чисел или некоторый универсальный закон природы? Хочется верить, во второе, ибо жизнь — это не хаос случайностей, а претворение генетически определенных законов. Видимо, действием закона золотого сечения в природе и объясняются интригующие проявления этого закона в искусстве. По крайней мере, автор стоит на "природнической" точке зрения на прекрасное и в законах искусства видит отражение законов красоты природы (хотя и те и другие законы пока еще не познаны).

Почему же закон золотого сечения так часто проявляется в архитектуре? Этому есть, на наш взгляд, вполне рациональное, математическое объяснение. Мы знаем, что для достижения гармонии в произведении искусства (в том числе и в архитектурном произведении) должен выполняться принцип Гераклита: "из всего — единое, из единого — все". В самом деле, гармония в архитектурном произведении зависит не столько от размеров самого сооружения, сколько от соотношений между размерами составляющих его частей. Для того чтобы выполнялся основной принцип гармонии "все во всем", взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение, т. е. архитектурное "целое" а и его части а 1, а 2, а 3, а 4, ... должны находиться в одинаковых отношениях

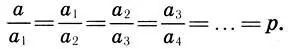
Отсюда a = a 1p, а 1=а 2р, а 2= а 3p, ..., или a 1= qa, a 2= q 2a, a 3= g 3a, ... (q = l/p), т. е. "целое" а и его части a 1, а 2, а 3, ... должны образовывать геометрическую прогрессию

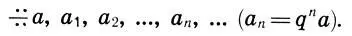(15.13)

Но части архитектурного целого должны "сходиться" в целое, т. е., разделив "целое" а на части а 1и а 2, необходимо, чтобы

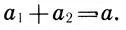
Учитывая (15.13), условие (15.14) примет вид

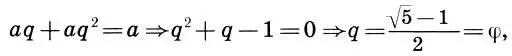
т. е. единственное положительное значение для q равно коэффициенту золотого сечения φ.

Итак, из всех геометрических прогрессий (15.13) только ряд золотого сечения обладает аддитивным свойством (15.14), поэтому только при делении "целого" a на части а 1и а 2в золотой пропорции выполняется принцип "все во всем" и одновременно части "сходятся" в целое.

Пропорции храма Василия Блаженного в Москве определяются восемью членами ряда золотого сечения: 1, φ, φ 2, φ 3, φ 4, φ 5, φ 6, φ 7

При этом соотношения (15.13) и (15.14) принимают вид (12.4)

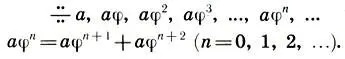
Это и есть знакомый нам ряд золотого сечения.

Подробным анализом пропорций некоторых архитектурных шедевров разных эпох, стилей и разных народов мы займемся в следующих двух главах. Но сейчас нам хочется закончить разговор о золотом сечении одним примером, показывающим, насколько органично входит оно в архитектурные пропорции. В качестве примера рассмотрим пропорциональный строй одной из жемчужин древнерусской архитектуры — храма Василия Блаженного в Москве. За "целое" а = 1 принята высота храма. Пропорции храма определяются восемью членами ряда золотого сечения:

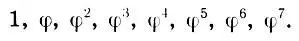
Многие из членов ряда неоднократно повторяются в пропорциях этого затейливого архитектурного сооружения, но всегда благодаря аддитивному свойству золотого сечения мы уверены в том, что части сойдутся в целое, т. е.

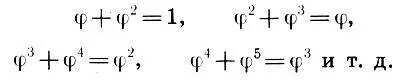
Таким образом, аддитивное свойство золотого сечения делает эту геометрическую пропорцию единственной и неповторимой.

"Человек — мера всех вещей..." Этот знаменитый афоризм древнегреческого философа-софиста Протагора (ок. 490 — ок. 420 до н. э.) является ключом к разгадке тайны пропорций Парфенона, его поразительной гармонии и спокойствия. Как это ни парадоксально, но между живыми линиями человеческого тела и застывшими на тысячелетия каменными очертаниями древнего сооружения существует глубокая связь, выраженная в математических законах пропорциональности. Но по порядку...