Александр Волошинов - Математика и искусство

"Сколько пар кроликов в один год от одной пары рождается?

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца своего рождения. Так как первая пара в первом месяце дает потомство, удвой, и в этом месяце окажется 2 пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; ..." И т. д. В заключение Фибоначчи пишет: "...мы складываем первое число со вторым, т. е. 1 и 2; и второе с третьим; и третье с четвертым; и четвертое с пятым; и так одно за другим, пока не сложим десятое с одиннадцатым, т. е. 144 с 233; и мы получим общее число упомянутых (пар.- А. В.) кроликов, т. е. 377; и так можно делать по порядку до бесконечного числа месяцев".

Заметим, что свое решение Фибоначчи дал для взрослой пары кроликов. Если же решать задачу для новорожденной пары, то мы получим полный ряд Фибоначчи (15.6) и к концу года будем иметь 233 пары кроликов.

Но какое отношение задача о размножении кроликов имеет к золотому сечению? А вот какое. Если мы возьмем отношение последующего члена ряда (15.6) к предыдущему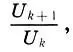

, то весьма скоро обнаружим, что это отношение с ростом k стремится к коэффициенту золотого сечения Φ. В самом деле,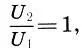

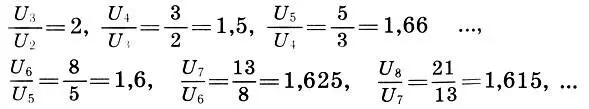
Поэтому, глядя на рисунок, нетрудно убедиться (хотя не так-то просто доказать!), что

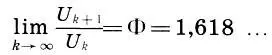(15.8)

и наоборот,

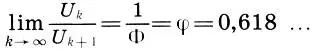(15.9)

Процесс асимптотического приближения отношения U k+1/U kк Φ напоминает затухающие колебания маятника.

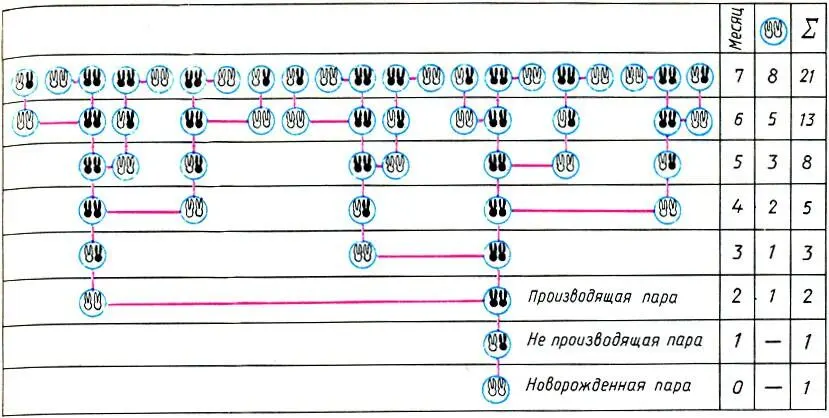
'Генеалогическое древо кроликов' в задаче Фибоначчи. Общее число пар кроликов, так же как и число новорожденных пар, образует последовательность чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21, ...

Рассмотрим цепную дробь

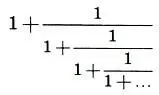
Обозначая эту дробь через х>0, нетрудно увидеть то же самое х в знаменателе первой дроби. Поэтому

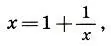
откуда находим уравнение для х:

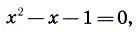
которое имеет единственный положительный корень

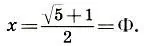
Итак, коэффициент золотого сечения Φ можно представить в виде цепной дроби

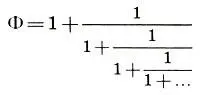(15.10)

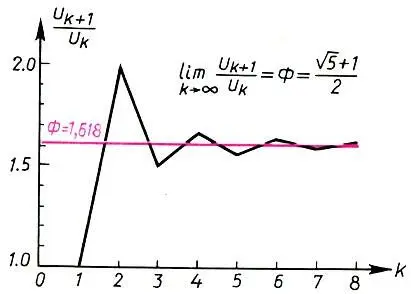
Для ряда Фибоначчи [U k] отношение U k+1/U kпоследующего члена ряда к предыдущему с ростом k стремится к коэффициенту золотого сечения Φ = (√5 + 1)/2

Выпишем подходящие дроби (см. с. 136) Цепной дроби (15.10):

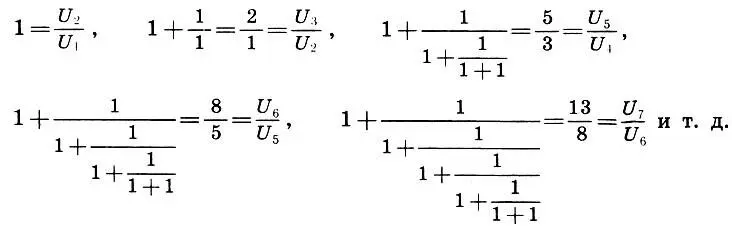
Как видим, подходящие дроби, которые являются рациональными приближениями иррационального числа Φ, равны отношениям соседних чисел Фибоначчи 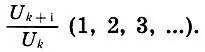Поэтому

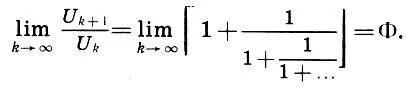
Итак, отношение двух соседних чисел Фибоначчи является рациональным приближением коэффициента золотого сечения , т. е.

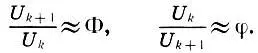
Именно таким рациональным приближением числа Φ и является интервальный коэффициент малой сексты (обращение большой терции 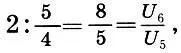, которым Гримм выражал отношение главных вертикалей Парфенона; см. с. 202). Другим примером рационального приближения числа Ф является отношение числа четвертей во второй и четвертой паре "проведение — интермедия" в фуге ре минор Баха (см. с. 165), которое в точности равно отношению 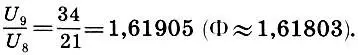. Еще раз обратим внимание на потрясающую точность (относительная погрешность составляет 0,06%!), с которой у Баха выполнен закон золотого сечения.

В 1843 г., через 641 год после открытия ряда Фибоначчи, определяемого рекуррентно через сумму двух предыдущих членов ряда, французский математик Ж. Бине нашел формулу для вычисления n-го члена ряда Фибоначчи как функции его номера:

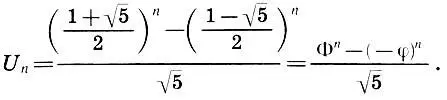(15.11)

Пользуясь формулой Бине (15.11) нетрудно доказать, что

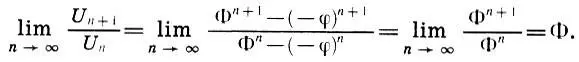
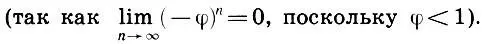
Наконец, укажем еще одно представление коэффициента золотого сечения Φ, полученное в начале нашего века:

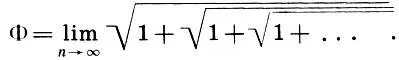(15.12)

Не правда ли, все формулы (15.10)- (15.12) отличаются особой красотой, простотой и изяществом!