Александр Волошинов - Математика и искусство

Гримм, воспитанный на целочисленных музыкальных пропорциях Возрождения, считает, что главные вертикали Парфенона находятся в отношении малой сексты (8/5). Казалось бы, совершенно иной, "музыкальный", подход. Но и здесь нет противоречия с Цейзингом и Жолтовским, ибо 8/5, как будет показано в следующей главе, есть отношение двух членов ряда Фибоначчи и является одним из рациональных приближений коэффициента золотого сечения Ф (8/5 = 1,600; Φ ≈ 1,618). Гримм правильно заметил, что золотое сечение в главных вертикалях Парфенона выдержано лишь приблизительно, и этим уточнил Цейзинга и Жолтовского.

Но все эти исследования носили эмпирический характер и не давали целостной системы античного пропорционирования. Первой такой попыткой была система динамических прямоугольников американского искусствоведа Хэмбиджа. Прямоугольники с иррациональным отношением сторон Хэмбидж называет динамическими, связывая с ними идею роста, движения и гармонии в природе и искусстве. Особую роль Хэмбидж отводит прямоугольнику с отношением сторон 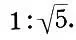. Хэмбидж разбивает фасад Парфенона на ряд динамических прямоугольников (l:√5) и квадратов (1:1). Здесь все ново и спорно: и подход, и метод, и чертеж. Но что будет с интересующими нас главными вертикалями? Выражая вертикальные элементы х, у, z через ширину основания а:х — а/2√5, у = а/4√5, z = а/4, легко видеть, что главные вертикали Парфенона по-прежнему находятся в золотой пропорции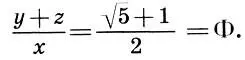

Метод пропорционирования немецкого теоретика Месселя основан на десятикрат ном делении окружности. Мессель считает, что обычный циркуль (или шнур) являлся основным рабочим инструментом античного и средневекового зодчего. Подход Месселя также оригинален и также спорен во всех аспектах, кроме одного — математического. Действительно, как мы увидим в следующей главе, при делении окружности на десять частей можно получить весь ряд золотого сечения (12.4)! Поэтому В 1С 1:С 1А 1= Φ ≈ВС:СА, т. е. интересующие нас главные вертикали Парфенона приблизительно находятся в золотой пропорции.

В главе 16 мы подробнее познакомимся с системой пропорционирования Шевелева и покажем, что в этой системе для главных вертикалей также приближенно выполняется золотая пропорция.

Заметим, что во всех случаях приближенного выполнения пропорции золотого сечения ошибка не превышает 1%. К сожалению, существующие обмеры Парфенона выполнены примерно с такой же точностью и поэтому не могут служить критерием истинности теории. Но и более тщательные обмеры Парфенона нужно будет осторожно применять в качестве критерия истины, ибо при строительстве сооружения 2500 лет назад, разумеется, могли быть допущены отклонения от замысла автора.

Вот почему главным критерием истинности той или иной гипотезы будет оставаться ее логическая непротиворечивость, ее математическая целостность. Этим требованиям, по нашему мнению, наиболее полно удовлетворяет система Шевелева, которая не получила еще должного признания. Система Шевелева позволяет из одного размера — ширины стилобата (верхней ступени основания) — получить все размеры Парфенона в диапазоне от 69,5 м (длина стилобата) до 16 см (высота шейки капители)! Таким образом, именно в системе Шевелева выполняется принцип гармонии Гераклита: "из всего — единое, из единого — все".

Итак, главный вопрос о том, какой системой пропорций пользовался гениальный создатель Парфенона зодчий Иктин, пока остается открытым. Заметим, что мы остановились только на соотношении двух главных вертикалей Парфенона. В золотой пропорции соотносятся и многие другие элементы Парфенона, однако подробный анализ пропорций этого великого архитектурного памятника занял бы объем, по крайней мере равный объему всей этой книги. Мы же в нашем кратком обозрении убедились, что разговор об архитектурных пропорциях неизбежно приводит к золотой, или, как ее называли во времена Возрождения, божественной пропорции. Поэтому нам необходимо подробнее познакомиться с математическими свойствами этого интереснейшего феномена.

Пятиконечной звезде — около 3000 лет. Ее первые изображения донесли до нас вавилонские глиняные таблички. Из Древней Вавилонии в Средиземноморье, как полагают, звездчатый пятиугольник перевез Пифагор и сделал его символом жизни и здоровья, а также тайным опознавательным знаком. В средние века пентаграмма "предохраняла" от "нечистой силы", что, впрочем, не мешало называть ее "лапой ведьмы". Вспомним гётевского "Фауста":

Сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира.

Чем же объясняется такая популярность звездчатого пятиугольника? Тем, что совершенная форма этой геометрической фигуры радует глаз и разум. Звездчатый пятиугольник буквально соткан из пропорций, и прежде всего золотой пропорции. Красота формы пентаграммы, вытекающая из внутренней красоты ее математического строения, была замечена еще Пифагором и с тех пор не устает радовать глаз художника и разум математика.

Рассмотрим подробнее свойства звездчатого пятиугольника. Прежде всего заметим, что уже первый этап его построения — деление окружности на пять равных частей — представляет собой прекрасный пример "обретения неочевидной истины". В самом деле, в то время как деление окружности на 3, 4 и 6 равных частей не представляет затруднений, разделить окружность на 5 равных частей не так-то просто. Вот почему задача о пятикратном делении окружности подробно разбирается в таких великих сочинениях "Начала" Евклида, "Альмагест" Птолемея, "Руководство к измерению" Дюрера [25] Полное название трактата Дюрера — "Руководство к измерению при помощи циркуля и линейки в линиях, плоскостях и целых телах, составленное Альбрехтом Дюрером и напечатанное на пользу всем любящим знания с надлежащими рисунками в 1525 году". .