Александр Волошинов - Математика и искусство

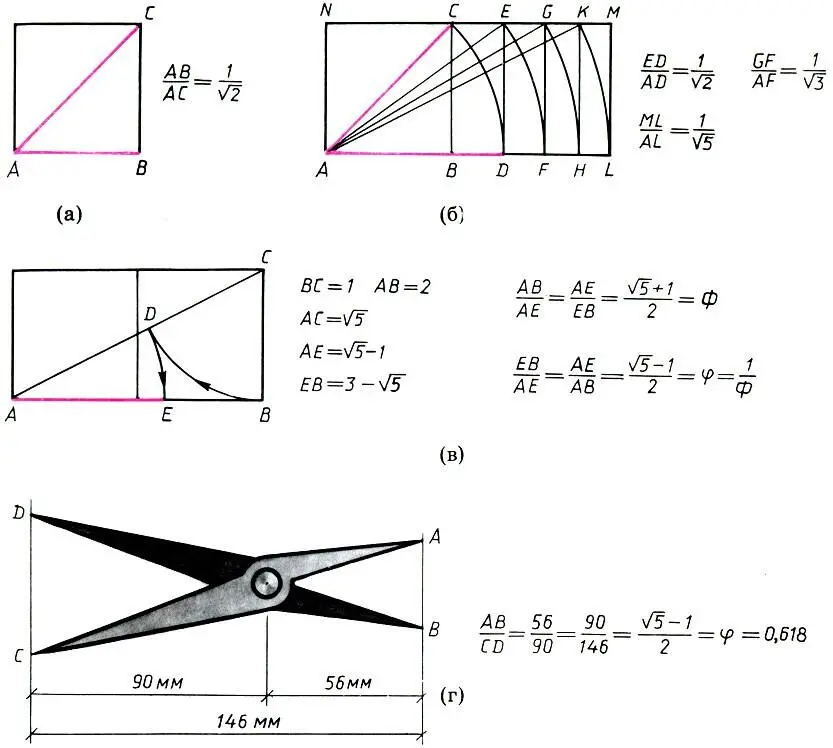
Примеры геометрического построения иррациональных отношений. Диагональ квадрата (а). Система прямоугольников с иррациональными отношениями сторон (б). Золотое сечение в системе 'двойной квадрат' (в). Помпейскйй пропорциональный циркуль, установленный на золотое сечение (г)

Зодчий Хесира. Фрагмент деревянной панели из гробницы Хесиры в Саккаре. XXVIII в. до н. э. Рельеф Хесиры — не только лучший образец древнеегипетского рельефного портрета, не только древнейшее в мире художественное произведение на дереве, но и научное свидетельство о древнеегипетской системе архитектурного пропорционирования

Существует и еще одно удивительное свидетельство мудрости древних. В Неаполе, в Национальном музее, хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных подлине ножек, скрепленных винтом наподобие ножниц, и позволяет (минуя вычисления!) для любого отрезка получать отрезок, находящийся с ним в заданном отношении. Действие пропорционального циркуля основано на подобии треугольников и не требует особых комментариев (г). Так вот, помпейский циркуль наглухо закреплен в отношении золотого сечения! Это легко проверить, зная размеры циркуля, которые на рисунке (г) указаны в миллиметрах.

Кроме помпейского, особый интерес представляет циркуль из Музея терм в Риме. Он также имеет длину вполовину римского фута — 146 мм, но настроен на другую иррациональную пропорцию (больший отрезок — 92 мм, меньший — 52 мм):

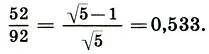
Геометрически эта пропорция означает отношение отрезка AD ко всей диагонали АС (см. с. 199). Как считает архитектор П. Ш. Шевелев, именно с помощью такого циркуля мог быть построен чертеж Парфенона.

Но, несмотря на многие доказательства, авторитет Витрувия (возможно, и неправильно понятого), авторитет модульной системы в архитектуре, был столь велик, что мысль о геометрическом построении иррациональных пропорций древними оформилась лишь к XX веку. Но как именно, по какой системе древние строили свои замечательные пропорции? Это по-прежнему оставалось тайной, и здесь теоретики архитектуры могли довольствоваться лишь гипотезами. Стремление познать тайны древних пропорций было огромным. Еще бы: ведь это дало бы ключ к созданию новых шедевров!

Естественно, что каждый автор стремился проверить свою теорию на пропорциях Парфенона. Парфенон был и остается совершеннейшим из архитектурных сооружений, архитектурной скульптурой, мраморным сводом законов античного зодчества. Уникальность и бессмертие Парфенона осознавали уже в античности. Вот как писал о Парфеноне в I веке древнегреческий писатель, историк и философ Плутарх (ок. 46 — ок. 127): "Так вырастали эти строения, гордые в своем величии, непревзойденные по своей волшебной красоте. Такими они были потому, что мастера старались превзойти друг друга, каждый из них свое ремесло превращал в художественное творчество... И так эти здания словно дышат молодостью, из века в век защищающей их от зуба времени. Можно сказать, что от этих творений веет ароматом каменных цветов и в них живет душа, которая никогда не стареет".

Теорий античных пропорций, и в частности пропорций Парфенона, становилось все больше. Наконец, к середине XX века их стало столько, что сами архитекторы перестали понимать, какие же из этих теорий справедливы и есть ли среди них таковые. Некоторые архитекторы вообще потеряли веру в пропорции. Вот, например, выдержка из книги архитектора Г. Б. Борисовского " Наука, техника, искусство":

"Все исследователи, почти как правило, дают анализ пропорций Парфенона,

стараясь привлечь его в качестве авторитетного свидетеля правоты их теории. Это делают Тирш, Цейзинг, Жолтовский, Гримм и др. Все ищут в нем именно тот порядок, который они отстаивают своей теорией. Если сопоставить эти анализы, то обнаружится несколько странная ситуация.

Тирш еще в прошлом столетии заявил: пропорции Парфенона построены на подобии. Вот чертеж, неоспоримо доказывающий это. (Чудесно,- говорят все.)

Цейзинг уверяет: в основе пропорций Парфенона лежит золотое сечение. Вот чертеж, это подтверждающий. (Все в восхищении.)

Жолтовский считает: Парфенон зиждется на золотом сечении. И дает совершенно иной чертеж, неоспоримо подтверждающий это. (Все в восторге.)

Гримм утверждает то же, что Цейзинг и Жолтовский, и приводит другой чертеж, не менее убедительный, хотя и совсем не похожий на два предыдущих. (Все в изумлении.)

Хэмбридж утверждает: пропорции Парфенона складываются из динамических прямоугольников. Вот чертеж, неоспоримо это доказывающий. (Все аплодируют.)

Мессель заявляет: пропорции Парфенона основаны на членении окружности. Вот чертеж, убеждающий нас в этом. (Аплодисменты, переходящие в овацию.)

Не так давно архитектор И. Шевелев опубликовал статью и небольшую книгу, в которой утверждает, что пропорции Парфенона основаны на соотношении 1:√5, и представляет чертеж с расчетом, убедительно это подтверждающим. (Аплодисментов пока не слышно.)

Явно здесь что-то не так ..."

Действительно, глядя на различные чертежи пропорций Парфенона, кажется, что между ними нет ничего общего. Между тем здесь все "так". Различные анализы пропорций Парфенона — это различные доказательства "теоремы Парфенона", которая, как и теорема Пифагора, имеет много доказательств. Но от этого "теорема Парфенона" не становится хуже (или вовсе перестает существовать, как кажется Борисовскому), а, напротив, предстает перед нами во всем своем богатстве и красоте. Ибо множество доказательств свидетельствует о большом числе конкретных реализаций, о "всеобщности" доказываемого, а всеобщность является одним из признаков красоты науки (см. с. 29, 30).

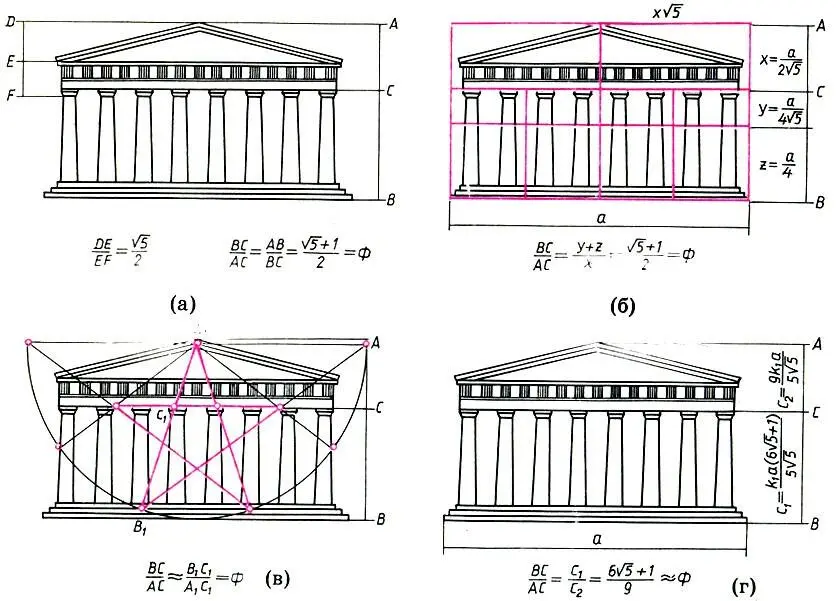
Различные методы анализа пропорций Парфенона: Жолтовский (а), Хэмбидж (б), Мессель (в), Шевелев (г)

В самом деле, Тирш говорит о подобии. Но подобие — это геометрическое выражение пропорциональности.

Цейзинг и Жолтовский уточняют: в пропорциях Парфенона имеется золотое сечение. В частности, в золотой пропорции соотносятся главные вертикальные размеры портика: высота ВС поддерживающих частей (основание и колонны) и высота АС поддерживаемых частей (антаблемент и фронтон).