Александр Волошинов - Математика и искусство

4. Отрезки пятиконечной звезды АВ = Φ, AD = 1, АЕ = φ и ED = φ 2связаны между собой всеми видами "древних" средних (5.1), а именно:

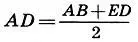
— арифметическое среднее;

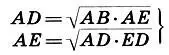
— геометрическое среднее;

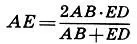
— гармоническое среднее.

В общем случае для четырех последовательных членов ряда (15.5) φ n, φ n+1, φ n+2, φ n+3нетрудно доказать справедливость соотношения

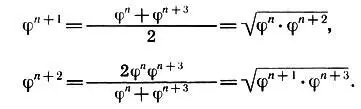
5. Из всех равнобедренных треугольников только треугольник, у которого углы при основании (72°) вдвое больше угла при вершине (36°), обладает особым свойством: биссектриса угла при основании делит противоположную сторону в золотом сечении. Такой треугольник (например, ΔАВС на с. 206) получил название "возвышенного".

Подведем некоторый итог: мы выполнили обещание, данное на с. 204 и показали, что пятиконечная звезда (пентаграмма) наряду с золотой пропорцией содержит все "древние" средние. Такое необычайно пропорциональное строение пентаграммы, красота ее внутреннего математического строения, по-видимому, и являются основой красоты ее внешней формы. Можно только догадываться, в какой восторг приводило пифагорейцев столь редкое обилие математических свойств в одной геометрической фигуре. Поэтому неудивительно, что именно пентаграмма была выбрана пифагорейцами в качестве символа жизни и здоровья.

Разделим теперь окружность на 10 равных частей. Это легко сделать с помощью описанного нами метода Птолемея (см. с. 205), в котором отрезок ОА дает сторону правильного десятиугольника (докажите это). Соединяя подряд точки деления окружности, получим правильный десятиугольник, а соединяя точки деления через две,- звездчатый десятиугольник. Внутри звездчатого десятиугольника вновь образуется правильный десятиугольник, в который можно вписать новый звездчатый десятиугольник, и т. д. (см. рисунок на с. 206).

Проведя радиусы в вершины десятиугольников, легко увидеть (именно увидеть глазами) целое созвездие пятиконечных звезд. А зная свойства последних, мы предчувствуем обилие золотых пропорций. Действительно, прежде всего заметим, что треугольник АОВ является возвышенным, поэтому АВ:ОВ = φ, т. е. сторона правильного десятиугольника а 10 относится к радиусу описанной окружности R в золотой пропорции а 10 :R = φ.

Далее, считая радиус исходной окружности R = l и учитывая свойства пятиконечной звезды, легко обнаружить весь ряд золотого сечения (15.5) в последовательности вписанных друг в друга звездчатых десятиугольников. В частности, на рисунке (б) ВС = φ, ОС = фφ 2, поэтому ВС/ОС = 1/φ = Φ (тем самым мы погасили еще один "долг" и доказали, что на рисунке ( в, с. 202) B 1C 1/C 1A 1= 0). Попутно мы чисто геометрическим путем доказали равенство

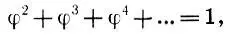
которое легко доказать и алгебраически, вспоминая формулу суммы бесконечно убывающей геометрической прогрессии

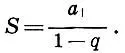
В нашем случае а 1=φ 2, q = φ, поэтому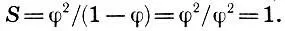

Заметим, что обнаруженное нами созвездие вложенных друг в друга пятиконечных звезд позволило сразу увидеть ряд золотого сечения при десятикратном делении окружности и избавило от громоздких алгебраических выкладок.

Теперь становится понятным, почему именно десятикратное деление окружности было выбрано Месселем в качестве метода архитектурного пропорционирования. При десятикратном делении окружности легко получить весь ряд золотого сечения (15.5), который играет огромную роль в архитектурных пропорциях.

Рассмотренные нами геометрические свойства золотого сечения в числе других были с восторгом описаны в 1509 г. в книге монаха ордена францисканцев Луки Пачоли (ок. 1445 — ок. 1514) "О божественной пропорции". Пачоли приводит лишь тринадцать свойств золотого сечения (дабы почтить двенадцать апостолов и их учителя Христа), отмечая, что для перечисления всех свойств золотого сечения не хватило бы чернил и бумаги. Каждому свойству золотого сечения Пачоли ставит особый эпитет, говоря "...о его третьем исключительном свойстве... о его четвертом невыразимом свойстве... о его десятом возвышенном свойстве... о его двенадцатом почти сверхъестественном свойстве...". Пачоли преподавал в различных университетах Италии и был талантливым педагогом. Любопытно, что хорошо известная каждому современному школьнику задача о трубах, наполняющих бассейн, описана в книге Пачоли "Сумма арифметики, геометрии, учения о пропорциях и отношениях", изданной в 1494 г.

Джакопо де Барбари. Портрет Луки Пачоли. Ок. 1510. Справа изображен ученик Пачоли Гвидобальдо д'Урбино. Возможно, это автопортрет художника. В левом верхнем углу подвешен ромбокубооктаэдр — одно из тел Архимеда. Справа на старинном фолианте стоит додекаэдр

Рассмотрим теперь ряд золотого сечения (15.4)

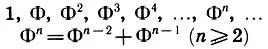
и, пользуясь аддитивным свойством ряда, будем выражать степени Φ nчерез Φ:

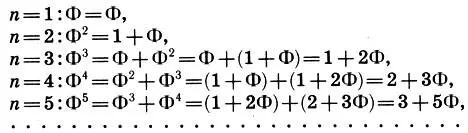
Легко видеть, что коэффициенты при Φ, также как и первые слагаемые, образуют последовательность натуральных чисел:

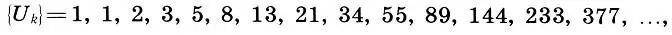(15.6)

каждый член которой, начиная с третьего, равен сумме двух предыдущих членов, т. е.

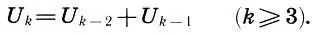(15.7)

Последовательности, в которых каждый член определяется как некоторая функция предыдущих, называются рекуррентными или возвратными .

Последовательность (15.6) имеет древнюю историю. Она впервые была описана в 1202 г. в "Книге об абаке" итальянским купцом и математиком Леонардо из Пизы, известным более по его прозвищу — Фибоначчи — сын доброй природы. С тех пор последовательность (15.6) называется рядом Фибоначчи, а ее члены — числами Фибоначчи. "Книга об абаке" Фибоначчи была своего рода математической энциклопедией средневековья и сыграла заметную роль в развитии математики в Европе. Значительную часть этого трактата составляли задачи, одна из которых гласила: