Александр Волошинов - Математика и искусство

Мы уже знаем о многих теориях античных пропорций, пытавшихся объяснить гармонию Парфенона на основе золотого сечения (см. гл. 14). Такой подход понятен ввиду особой роли золотого сечения как в природе, так и в искусстве, роли, которая во многом еще остается загадочной. Кроме того, апологеты золотого сечения ссылались на некоторые высказывания Платона о пропорциях. Однако эти высказывания великого философа, видимо, понимались слишком узко (см. с. 195). В главе 14 мы показали, что многие внешне различные теории пропорций Парфенона математически приводят к золотому сечению в отдельных элементах этого архитектурного шедевра. Но целостной теории на базе золотого сечения все-таки не получалось.

Некоторых исследователей отсутствие единой теории античных пропорций вообще разуверило в принципе пропорциональности. Пессимисты подняли на щит высказывание великого теоретика пропорций XX века Ле Корбюзье о том, что "Парфенон — это более, чем архитектура, это — скульптура". Они объявили математическое исследование пропорций Парфенона кощунством. Действительно, тщательное изучение показало, что в Парфеноне, как и в человеческом теле, нет прямых линий. Линии Парфенона наполнены жизнью и пластикой. Однако это отнюдь не означает, что в них нет пропорциональной зависимости, той самой, которую так одержимо искали и находили в теле человека Поликлет, Леонардо да Винчи, Дюрер и др.

А оптимисты продолжают поиск законов строения архитектурных шедевров, поиск тех вечных истин, которые, возможно, являются общими законами формообразования и в природе, и в искусстве. Оригинальную теорию разрабатывает в течение последних двадцати лет архитектор И. Ш. Шевелев. Это теория парных мер, которая настолько естественна, что просто удивительно, почему она до середины XX века никому не пришла в голову. Парные меры - это два эталона длины а и Ь, которые позволяли устанавливать одинаковые отношения между отдельными парами архитектурного сооружения a:b = na:nb (n = 1, 2, 3, ...). Какие же величины выступали в качестве парных мер? Сама история развития математики указывает на то, что это были геометрические объекты: сторона и диагональ прямоугольника. В самом деле, математика начиналась с геометрии, а слово "геометрия" означает землемерие. Основной задачей последнего было измерение площадей земельных участков. Древнейшим методом измерения площадей был метод приложения , суть которого состояла в следующем. К измеряемому прямоугольнику прикладывается эталон площади (как правило, квадрат). В прямоугольнике, образованном стороной эталона и стороной измеряемого участка, проводилась диагональ до пересечения с продолжением второй стороны эталона.

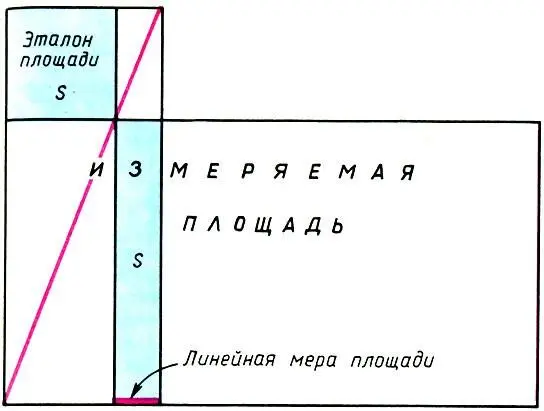
Измерение площади прямоугольного участка 'методом приложения'

Получалось три прямоугольника. Два из них, через которые прошла диагональ, подобны, а третий равновелик эталону (докажите это). Сторона равновеликого прямоугольника и служила линейной мерой для определения площади. Так измерение площади сводилось к простому подсчету числа линейных мер в стороне измеряемого прямоугольника. Так сторона и диагональ прямоугольника становились основными инструментами древних землемеров-математиков.

Из всего множества прямоугольников квадрат и двойной квадрат обладают тем практическим преимуществом, что требует для построения прямого угла не три, а две меры (в двойном квадрате большая сторона получается двукратным отложением малой). Так появились парные меры 1:√2 и 1:√5 (см. с. 199).

Знания, накопленные в геометрии, использовались и в архитектуре. Древние зодчие были прекрасными математиками. Но в отличие от землемерия архитектура обладает третьим измерением — высотой. Поэтому стороны и диагональ прямоугольника, проведенные на земле, пришлось заменить мерными палками, которыми можно было оперировать и в третьем измерении. Парную меру двойного квадрата 1:√5 мы и видим в руках древнеегипетского зодчего Хесиры (см. с. 200).

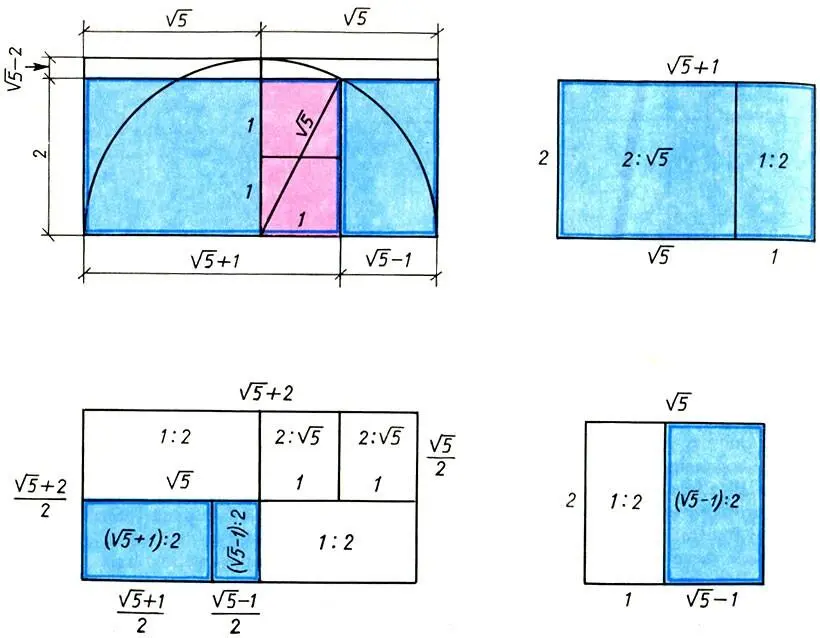
Геометрические свойства системы двух квадратов. Исходный двойной квадрат показан красным, прямоугольники золотого сечения — синим. Рисунок демонстрирует также аддитивное свойство прямоугольников системы двойного квадрата

Парная мера 1:√5 встречается во множестве древних сооружений, разделенных между собой веками и тысячами километров: пирамиды Джосера, Хеопса, Хефрена и Миккерина, пропорции Парфенона и Эрехтейона, церковь Покрова на Нерли и храм Вознесения в Коломенском, древние храмы Киева и Новгорода...

Разумеется, причина популярности этой парной меры не только в том, что для построения прямого угла с ее помощью требуются именно две, а не три меры. Истинная причина заключена в разнообразии математических свойств двойного квадрата.

В самом деле, возьмем квадрат со стороной 1, построим двойной квадрат (т. е. прямоугольник со сторонами 1 и 2), проведем в нем диагональ и опишем ею полуокружность (см. рис. ). Так мы построим новый двойной квадрат с малой стороной √5. Продлив стороны исходного двойного квадрата до пересечения со сторонами нового, мы получим целую гамму пропорций, содержащую практически все коэффициенты пропорциональности от 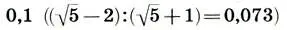до 1 с шагом 0,1:

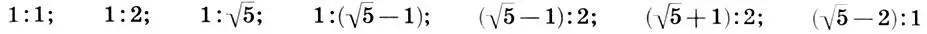
и т. д. Заметим: двойной квадрат тесно связан с золотым сечением. Так, в результате наших построений мы получили два прямоугольника золотого сечения, выделенные синим цветом: 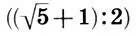и .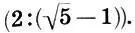

Ну а какое отношение математика двойного квадрата имеет к архитектуре? Широкое распространение в архитектуре пропорции двойного квадрата, как и пропорции золотого сечения, получили благодаря свойству, которое по аналогии с золотым сечением можно назвать аддитивным свойством площадей. Дело в том, что каждое архитектурное произведение или его часть можно вписать в прямоугольник. Так вот, прямоугольники системы двойного квадрата могут без остатка разлагаться на другие прямоугольники этой же системы. Это и есть аддитивное свойство площадей системы двух квадратов, аналогичное линейному аддитивному свойству золотого сечения. Например, прямоугольник золотого сечения ( 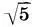+1) одной линией можно разделить на два прямоугольника, стороны которых будут относиться как 1:2 и 2: 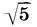, а прямоугольник со сторонами 2 и 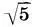легко разложить на "золотой" прямоугольник ( 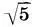-1):2 и двойной квадрат 1:2. Прямоугольник 1:2 четырьмя линиями разбивается на шесть прямоугольников: два неравных прямоугольника 1:2, два равных прямоугольника 2: √5 и два неравных "золотых" прямоугольника (√5 — 1): 2. И т. д. Таким образом, система двух квадратов дает поразительное разнообразие разбиений целого на части, находящиеся в тех же пропорциональных отношениях. Так, благодаря аддитивному свойству площадей системы двух квадратов достигается взаимосвязь целого и его частей, осуществляется основной принцип гармонии: "из всего — единое, из единого — все".