Александр Волошинов - Математика и искусство

Заметим, что получаемые в системе Двух квадратов прямоугольники с отношением сторон 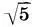:2≈1,118 близки к квадратам, а само отношение √5:2 представляет так называемую функцию золотого сечения , введенную архитектором Жолтовским. В терминах ряда золотого сечения (15.5) функция золотого сечения определяется как отношение

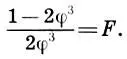
Поскольку 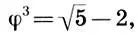, то мы легко получаем

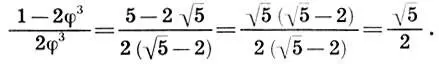
Прямоугольник с отношением сторон 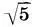:2 Жолтовский называл "живым квадратом", считая, что он должен заменить в архитектуре математический квадрат, который не встречается в природе и не радует глаз своей пропорцией (1:1). Будучи большим энтузиастом золотого сечения и его функции, Жолтовский нашел многочисленные примеры этих пропорций в архитектурных шедеврах, в том числе и в Парфеноне (см. с. 202). Итак, среди многих пропорций, обладающих аддитивным свойством площадей, двойной квадрат содержит и такие "выдающиеся" пропорции, как золотое сечение и функцию золотого сечения.

Теория парных мер родилась в 60-е годы. Однако, кроме мерных палок Хесиры, эта теория реальных подтверждений не имела и, по существу, оставалась гипотезой, построенной на математических рассуждениях. Правда, пропорциональные циркули (см. с. 199) также представляют собой парные меры. Но это меры, с помощью которых строился чертеж архитектурного сооружения, а не само сооружение. И вот в 1970 г. теория парных мер получила еще одно блестящее доказательство. При археологических раскопках в Новгороде экспедицией члена-корреспондента АН СССР А. В. Арциховского был найден обломок мерной трости конца XII века. Мерная трость представляет собой брусок прямоугольного сечения, на трех гранях которого нанесены три различные шкалы. 24 деления каждой из шкал дают разные сажени: тмутараканскую (С т= 142,1 см), мерную (С м= 175,6 см) и косую новгородскую (К н= 200,9 см). Но ведь это не что иное, как парные меры системы двух квадратов! В самом деле, С т: С м= 1:( 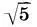— 1) = 0,809, С т:К н= 1:√2 = 0,707. (Подробнее о древнерусских парных мерах и системах пропорционирования мы поговорим в следующей главе.) Так мерная трость [26] Первые упоминания о мерной трости имеются в библейских текстах, рассказывающих о строительстве храма царя Соломона и относящихся к X веку до н. э. , а вместе с ней и парные меры из математических абстракций перешли в область реального. Так в нетрадиционной области — теории архитектуры — еще раз проявилось удивительное свойство математики совершать открытия "на кончике пера". Так геометрия двойного квадрата связала воедино мерные палки Хесиры, античные пропорциональные циркули и новгородскую мерную трость.

Вернемся, наконец, к теории пропорций Парфенона, к афоризму Протагора: "человек — мера всех вещей". Для древнегреческой философии, искусства и религии всегда было характерно очеловечивание сил природы — антропоморфизм . Даже греческие боги были подвержены человеческим слабостям и страстям. Архитектура в антропоморфизме греков не составляла исключения. Вот что по этому поводу писал тонкий знаток античной архитектуры, профессор Н. И. Врунов: "Ордер классического греческого храма является также главным носителем человеческого начала: он осуществляет на языке архитектуры образ монументализированного человека-героя... Самая форма дорической колонны вызывает ассоциации, связанные с человеческим телом. Прежде всего — вертикализм колонны. Вертикаль — главная ось человеческого тела, основная характерная особенность внешнего облика человека, главное его отличие от облика животного".

Но какой именно математической зависимостью связаны пропорции дорической колонны и человеческого тела? В поисках ответа на этот вопрос роковую роль сыграло следующее высказывание Витрувия: "Желая сделать так, чтобы они (колонны.- А. В.) были пригодны к поддержанию тяжести и обладали правильным и красивым обличьем, они измерили след мужской ступни по отношению к человеческому росту, и, найдя, что ступня составляет шестую его долю, применили это соотношение к колоннаде, и, сообразно с толщиной основания ее ствола, вывели ее высоту в 6 раз больше, включая сюда и капитель. Таким образом, дорийская колонна стала воспроизводить в зданиях пропорции, крепость и красоту мужского тела". Итак, по Витрувию, справедливы отношения: (стопа человека): (высота его тела) = (диаметр колонны): (общая высота колонны) = 1:6. Между тем обмеры дорических колонн упрямо противоречили Витрувию. Неумолимые цифры заставили Брунова отказаться от своих прежних воззрений: "Нельзя утверждать, что дорическая колонна повторяет пропорции тела человека, потому что людей таких пропорций, как колонны Парфенона, не существует". Разгадка была где-то рядом, но ее нашел только в 60-е годы архитектор Шевелев. Вот его решение.

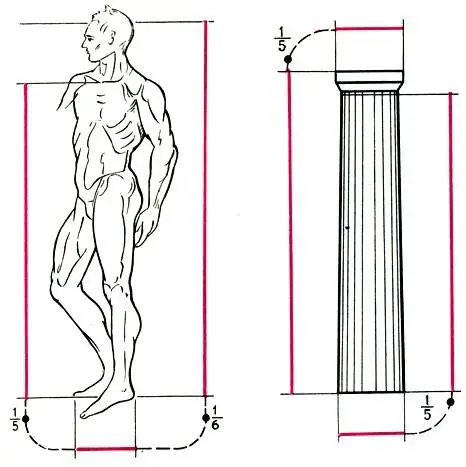
Отношение длины стопы человека к длине его тела от основания шеи до стопы 1:5 — ключ к пропорциональному строю Парфенона (по Шевелеву)

Со времен Поликлета установлено, что если стопу человека принять за единицу измерения — фут (греческий фут = 30,89 см), то рост человека составит 6 футов, а голова вместе с шеей — 1 фут. В этом можно убедиться, глядя на рисунок на следующей странице. Следовательно, на оставшуюся часть тела приходится 5 футов. Именно эта часть и олицетворяет "крепость и красоту мужского тела". В самом деле, в "человеческой колонне" шея — самое слабое место. Груз взваливают на плечи, и даже атланты сгибают шеи и принимают тяжесть на поднятые к голове руки. Эта простая мысль и привела Шевелева к тому, что ствол колонны, несущий тяжесть, должен ассоциироваться не с полным ростом человека, а с его наиболее крепкой частью от стоп до основания шеи. Все сразу стало на свои места. Возникла цепочка пропорций, выполнявшихся с прекрасной точностью:(нижний диаметр колонны):(высота ствола колонны)=(ширина капители по абаке):(высота колонны с капителью) = (стопа человека):(высота человека от стоп до основания шеи)=1:5. Далее, поскольку "подобное в мириады раз прекраснее того, что неподобно" (Витрувий), отношение 1:5 было распространено на всю соразмерность колоннады в целом: (высота колоннады = колонна + антаблемент):(длина храма по стилобату)=1:5.