Сергей Гашков - Примени математику

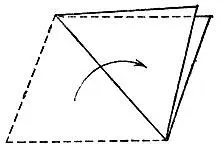
Рис. 109

Можно ли гарантировать, что этот кусок материи имеет форму квадрата?

18.7. Еще одна "проверка квадратности"Четырехугольный кусок материи перегнули так, что две его противоположные стороны точно совместились (рис. 110). Затем материю развернули и перегнули так, что две другие противоположные стороны точно совместились.

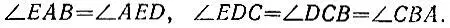
Рис. 110

Можно ли гарантировать, что этот кусок материи имеет форму квадрата?

18.8. Перегибания квадратаКакое наименьшее количество раз необходимо перегнуть четырехугольный кусок материи, чтобы убедиться в том, что он имеет форму квадрата?

18.9. Перегибания кругаКусок материи перегнули по некоторой линии и убедились в точном совмещении двух образовавшихся в результате частей. Затем материю развернули, перегнули по некоторой другой линии и снова убедились в совмещении частей и т. д. Можно ли после нескольких таких проверок гарантировать, что этот кусок материи имеет форму круга?

18.10. Параллельность прямыхМожно ли с помощью перегибаний куска материи убедиться в том, что два края этого куска параллельны? Как установить, имеет ли данный кусок материи форму трапеции или параллелограмма?

18.11. Перпендикулярность прямыхКусок материи имеет форму треугольника. Как, перегибая материю, установить, является ли этот треугольник прямоугольным, остроугольным или тупоугольным?

18.12. Вертикальность шестаНа недоступном для вас возвышении установлен длинный шест. Как с помощью отвеса проверить его вертикальность?

18.13. Вогнутость и выпуклость поверхностиДля того чтобы проверить, нет ли на гладкой поверхности стола каких-либо вогнутостей, можно натянуть руками обыкновенную нитку и, прижимая пальцами ее концы к разным точкам стола, установить, нет ли просвета между ниткой и поверхностью (рис. 111).

Рис. 111

На чем основана эта проверка? Годится ли она для отыскания на гладкой поверхности стола каких-либо выпуклостей?

18.14. Перпендикулярность плоскостейВы хотите проверить, перпендикулярны ли друг другу соседние стены в вашей комнате. Как воспользоваться для этого теоремой Пифагора?

18.15. Параллельность плоскостейВы хотите проверить, параллельны ли друг другу стены коридора. Нельзя ли это сделать с помощью измерительной ленты или просто достаточно длинной палки?

18.16. Признаки трапецииКакие из следующих действий имеет смысл выполнить, чтобы однозначно установить параллельность двух данных противоположных сторон четырехугольника:

а) соединить отрезком середины двух данных сторон и убедиться в том, что этот отрезок проходит через точку пересечения диагоналей четырехугольника;

б) проверить, что полусумма двух данных сторон равна расстоянию между серединами двух других сторон четырехугольника?

Используя ответ на предыдущий вопрос задачи, придумайте способ проверки того, что данный четырехугольник является трапецией.

18.17. Признаки параллелограммаКакие из следующих свойств четырехугольника выполнены в том и только в том случае, если этот четырехугольник является параллелограммом:

а) противоположные стороны четырехугольника попарно равны;

б) две противоположные стороны четырехугольника равны, а две другие его стороны параллельны;

в) каждая из диагоналей четырехугольника делится точкой их пересечения пополам?

18.18. Ромб ли это?На плоскости даны четыре точки А, В, С, D, про которые известно только, что AB = BC = CD = DA. Можно ли утверждать, что точки А, В, С, D являются вершинами некоторого ромба?

18.19. Признаки прямоугольникаДостаточно ли для проверки того, что все углы данного четырехугольника являются прямыми, установить одно из следующих свойств:

а) равенство двух противоположных сторон четырехугольника и равенство его диагоналей;

б) попарное равенство противоположных сторон и равенство его диагоналей;

в) равенство всех четырех отрезков, на которые разбиваются диагонали четырехугольника точкой их пересечения?

18.20. Признаки квадратаКакие из следующих свойств четырехугольника выполнены в том и только в том случае, если этот четырехугольник является квадратом:

а) равенство всех четырех сторон четырехугольника;

б) равенство всех четырех сторон четырехугольника и равенство его диагоналей;

в) равенство трех сторон четырехугольника и равенство его диагоналей?

18.21. Правильность равностороннего многоугольникаПусть все стороны многоугольника равны между собой. Будет ли он обязательно правильным, если выполнено одно из следующих условий:

а) около этого многоугольника можно описать окружность;

б) в этот многоугольник можно вписать окружность?

18.22. По одним лишь диагоналямВерно ли, что если в пятиугольнике равны все пять диагоналей, то он является правильным?

18.23. Правильность пятиугольникаПусть все стороны выпуклого пятиугольника равны между собой. Устанавливая равенство каких-то из его диагоналей, вы хотите убедиться в том, что этот пятиугольник является правильным.

Какое наименьшее число диагоналей вам нужно проверить?

18.24. О правильности и неправильностиДокажите, что если в выпуклом шестиугольнике равны все стороны, а все три его главные диагонали (т. е. такие, которые разбивают его на два четырехугольника) пересекаются в одной точке, то этот шестиугольник может и не быть правильным. Будет ли он правильным, если добавить одно из следующих условий:

а) каждая из главных диагоналей делится точкой их пересечения пополам;

б) все шесть отрезков, на которые разбиваются главные диагонали точкой их пересечения, равны между собой;

в) все три главные диагонали равны между собой, а все его неглавные диагонали разбиваются на тройки равных диагоналей, образующих треугольники?

18.25. Правильность шестиугольникаПусть все стороны выпуклого шестиугольника равны между собой. Устанавливая равенство каких-то из его диагоналей, вы хотите убедиться в том, что этот шестиугольник является правильным.

Какое наименьшее число диагоналей нужно проверить?