Сергей Гашков - Примени математику

18.17.Заметим, что если четырехугольник ABCD является параллелограммом, то все свойства, перечисленные в пп. а), б), в) условия задачи, для него выполнены. Пусть теперь AB = CD и AD = BC (рис. 127), тогда треугольники ABC и ADC равны по трем сторонам, откуда

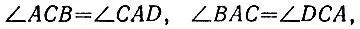
т. е. противоположные стороны четырехугольника ABCD попарно параллельны. Итак, свойство а) является и необходимым, и достаточным для параллелограмма.

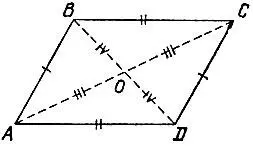
Рис. 127

О свойстве б) этого сказать нельзя, поскольку оно выполняется не только для параллелограмма, но и для любой равнобедренной трапеции (докажите, что ни для каких других выпуклых четырехугольников оно не выполняется).

Наконец, свойство в) является достаточным для того, чтобы объявить четырехугольник ABCD параллелограммом, поскольку равенство отрезков АО и СО, а также ВО и DO (рис. 127) влечет за собой равенство треугольников АОВ и COD, а также AOD и ВОС, откуда в свою очередь вытекает равенство противоположных сторон четырехугольника.

18.18.Для ответа на поставленный в задаче вопрос достаточно проверить, что замкнутая ломаная ABCDA ограничивает четырехугольник, который, согласно определению ромба, уже и будет ромбом. Действительно, так как равнобедренные треугольники ABC и ADC равны, то точки В и D находятся по разные стороны относительно прямой АС (иначе эти точки просто совпали бы друг с другом). Поэтому отрезок АВ не пересекается с отрезком CD, а отрезок AD не пересекается с отрезком ВС, т. е. ломаная ABCDA несамопересекающаяся, а, значит, ограничивает настоящий ромб ABCD.

18.19.Свойство, описанное в п. а), не является достаточным для того, чтобы объявить четырехугольник прямоугольником, поскольку это свойство выполняется также и для любой равнобедренной трапеции (докажите, что ни для каких других выпуклых четырехугольников оно не выполняется).

Свойства б) и в) достаточны, чтобы объявить четырехугольник прямоугольником. Действительно, из попарного равенства противоположных сторон четырехугольника вытекает, что он является параллелограммом (см. задачу 18.17), откуда получаем, что его диагонали делятся точкой их пересечения пополам, причем если сами диагонали равны, то равны и их половинки. Итак, из свойства б) вытекает свойство в). Наконец, если для четырехугольника выполнено свойство в), то точка О пересечения его диагоналей равноудалена от его вершин. Это означает, что точка О является центром описанной около четырехугольника окружности, а его диагонали являются диаметрами этой окружности, на которые опираются вписанные углы при вершинах четырехугольника. Следовательно, все эти углы прямые, что и требовалось доказать.

18.20.Заметим, что для квадрата выполняются все свойства а), б), в), перечисленные в условии задачи. Однако свойство а) выполняется не только для квадрата, но и вообще для любого ромба (и только для него, согласно задаче 18.18). Свойство в) выполняется также и для любой равнобедренной трапеции, у которой одно из оснований равно боковой стороне (докажите, что ни для каких других выпуклых четырехугольников оно не выполняется). Наконец, если для четырехугольника выполнено свойство б), то этот четырехугольник является ромбом (см. задачу 18.18) и прямоугольником (см. задачу 18.19) одновременно, а значит, и квадратом.

18.21.Вписанный равносторонний многоугольник обязательно является правильным (см. задачу 15.1), а вот описанный - не обязательно. Например, любой ромб, в который всегда вписывается окружность (так как его центр симметрии равноудален от всех четырех сторон), является равносторонним, но не правильным четырехугольником.

Полезно знать все же, что для правильности описанного нечетноугольника достаточно (и, разумеется, необходимо), чтобы он был равносторонним. Например, вершины А и С (расположенные через одну на рис. 128) равностороннего описанного пятиугольника равноудалены от центра О вписанной в него окружности. Действительно, так как АВ = ВС и DB = BE (отрезки касательных к окружности, проведенных из одной точки В, равны), откуда AD = EC , и раз OD = OE и ∠ ADO = ∠ CEO = 90° , то треугольники ADO и CEO равны. Двигаясь от вершины А через одну, мы перечислим все вершины пятиугольника, которые, таким образом, будут все равноудалены от точки О. Поэтому указанный пятиугольник одновременно является вписанным и, стало быть, правильным.

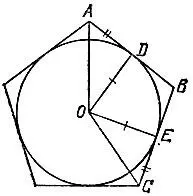
Рис. 128

18.22.Пятиугольник с равными диагоналями не обязательно правилен. Это утверждение подтверждается пятиугольником AEDCB, построенным следующим образом (рис. 129): пусть в равнобедренном треугольнике ADB угол при вершине D меньше 36°, тогда проведем перпендикуляры к прямой АВ, удаленные от точки D на расстояние, равное половине AD, и выберем на них точки С и Е, удаленные от точек А и В соответственно на расстояние AD, В построенном пятиугольнике все пять диагоналей равны между собой (по построению они равны диагонали AD), однако сам пятиугольник не является правильным, поскольку угол между диагоналями, выходящими из одной вершины правильного пятиугольника, равен 36°, а у нас получилось неравенство

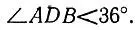
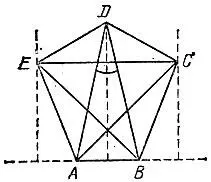
Рис. 129

Заметим, что более убедительным, хотя и менее строгим примером может служить вырожденный пятиугольник AEDCB со слившимися вершинами А и В, изображенный на рис. 130 и полученный из равностороннего треугольника АЕС добавлением еще одной вершины D, удаленной от вершины А на расстояние АС, и раздвоением вершины А на две вершины А и В.

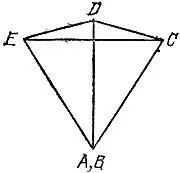
Рис. 130

Приемом построения вырожденных контрпримеров мы воспользуемся при решении следующих задач, а при желании вы сможете сами слегка подправить построения так, чтобы они были невырожденными.

18.23.Наименьшее число равных диагоналей, необходимых для проверки правильности равностороннего пятиугольника ABCDE, равно трем. Действительно, двух равных диагоналей для этого недостаточно: пример вырожденного пятиугольника, превратившегося в трапецию с равными диагоналями BD и СЕ, изображен на рис. 131.

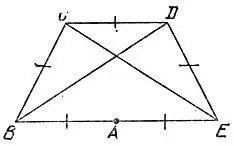
Рис. 131