Сергей Гашков - Примени математику

Какое наименьшее число сравнений является заведомо достаточным, если количество предметов равно: а) 3; б) 4; в) 5?

19.48. Формула для максимумаПредположим, что калькулятор имеет помимо четырех арифметических операций также и операцию взятия абсолютной величины числа. Придумайте формулу, по которой на этом калькуляторе можно найти наибольшее из двух произвольных чисел.

19.49. Перевозка ящиковВес нескольких ящиков с грузом в общей сложности составляет 10 т, причем каждый ящик весит не более 1 т . За какое наименьшее количество поездок трехтонная машина заведомо сможет перевезти весь этот груз?

19.50. На неправильных весахВы хотите отвесить 2 кг сахару на неравноплечих чашечных весах с помощью одной килограммовой гири. Подумайте над вопросом: больше или меньше 2 кг сахару вы получите, если отвесите 1 кг на одной чашке весов и еще 1 кг на другой? Можно ли на таких весах отвесить ровно 2 кг ?

19.51. Простейшие весыЗнаете ли вы, что весы можно изготовить из самой обыкновенной линейки с делениями для взвешивания, на которой нужна всего одна гиря? Если не знаете, то придумайте, как это сделать.

19.52. Сверка часовВы хотите установить более точное время на стенных часах в вашем доме. Ближайшие часы находятся в нескольких минутах ходьбы и показывают правильное время, однако отнести туда стенные часы вы не можете.

Как поступить?

19.53. Распределение работыОдна машинистка печатает страницу текста в среднем за 6 минут, а другая - за 10 минут. В каком отношении нужно распределить между ними работу по печатанию рукописи, чтобы эта работа была завершена в кратчайшее время? i

19.54. Без замены шинЗная, через сколько километров пути стираются шины на передних и задних колесах легкового автомобиля, придумайте способ, как максимально удлинить его пробег, не заменяя шин ни на одном из четырех колес автомобиля.

19.55. Суммарный эффектВнедрение одного изобретения сокращает производственные затраты на 50%, второго - на 40%, а третьего - на 10%, На сколько процентов позволит сократить производственные затраты внедрение всех трех изобретений сразу?

19.56. Постоянное пастбищеНа лугу растет трава. На этот луг пустили 30 коров, которые за 4 дня съели всю траву. Когда на лугу снова выросла трава, на него пустили 25 коров, которые съели всю траву за 6 дней. Какое наибольшее количество коров может пастись на лугу все время (пока вообще растет трава)?

19.57. Обойдя вокругПарашютист приземлился ночью около стены, окружающей некоторый участок земли в форме многоугольника. Пройдя вдоль всей стены и замерив какие-то углы, парашютист определил, где он находится: внутри участка или снаружи.

Как он это выяснил?

19.58. Как установить табуреткуПол в вашей комнате не очень ровный, зато табуретка совершенно ровная, т. е. нижние концы ее ножек лежат в одной плоскости и образуют квадрат. Как наиболее простым способом установить табуретку, чтобы она не качалась?

19.59. Диагональ кирпичаДля того, чтобы найти длину главной диагонали кирпича, т. е. расстояние между наиболее удаленными его вершинами, можно измерить линейкой, например, длину, ширину и высоту кирпича, а затем воспользоваться теоремой Пифагора. Предложите способ измерения линейкой главной диагонали, не требующий никаких вычислений.

19.60. Диаметр проволокиКак измерить с помощью линейки диаметр очень тонкой проволоки?

19.61. Не разматывая рулонБумажная лента свернута в рулон. Как с помощью линейки определить примерную длину ленты, не разматывая весь рулон целиком?

19.62. Радиус пластинкиУ вас в руках оказался осколок круглой пластинки. Можно ли по этому осколку определить радиус целой пластинки?

19.63. Объем шараКак с помощью измерительной ленты (сантиметра) определить объем данного шара?

19.64. С маякаКак далеко видно с маяка данной высоты над уровнем моря?

19.65. Радиус шараУ вас есть циркуль, линейка, карандаш и бумага. Можете ли вы с их помощью построить отрезок, равный радиусу бильярдного шара, помня, конечно, что прямые линии на сфере рисовать невозможно.

19.66. Наибольший участокВам нужно отгородить забором фиксированной длины прямоугольный участок. Каким должен быть этот участок, чтобы его площадь была наибольшей?

19.67. Наибольший палисадникУ стены дома нужно разбить прямоугольный палисадник, отгородив три его стороны забором фиксированной длины. При каком отношении этих сторон площадь палисадника будет наибольшей?

19.68. Наибольшая коробкаИз квадратного листа картона нужно сделать коробку, отрезав от каждого из углов по квадратику (на рис. 138 эти квадратики заштрихованы) и загнув боковые стенки. Каким должно быть отношение высоты коробки к стороне ее основания, чтобы объем коробки был наибольшим?

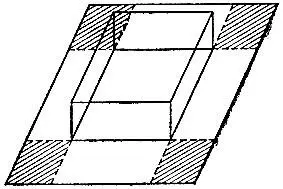
Рис. 138

19.69. Оптимальная формаВсе вы видели, как устроен обычный спичечный коробок: он имеет в общей сложности 2 торцевые стенки, 1 крышку, 2 дна и 4 боковые стенки (рис. 139). Какой должна быть форма коробка с фиксированным объемом, чтобы на его изготовление затрачивалось наименьшее количество материала?

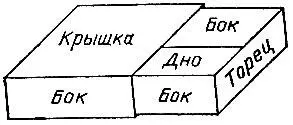
Рис. 139

19.70. ЭлектропроводкаТребуется соединить стенной проводкой выключатель и лампочку в зале длиной 30 м , а шириной и высотой по 12 м (рис. 140). Выключатель находится посреди торцевой стены на высоте 1 м от пола, а лампочка находится посреди противоположной стены на расстоянии 1 м от потолка.

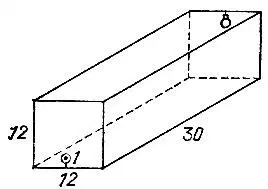
Рис. 140

По какому кратчайшему пути должна проходить проводка?

19.71. Не пробивая стенкуНа внутренней стенке открытого сверху цилиндрического бункера, сечение которого имеет длину окружности 6 м, а высота которого равна 4 м, находится лампочка на расстоянии 1 м от верха. Напротив лампочки снаружи бункера на высоте 1 м от пола находится выключатель (рис. 141).

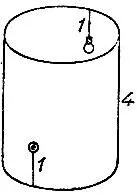
Рис. 141

Какой наименьшей длины провод нужен для проведения стенной проводки между выключателем и лампочкой, не пробивая стенку?

19.72. Не мала ли салфетка?Можно ли завернуть единичный кубик в квадратную салфетку размером 3*3 ?