Сергей Гашков - Примени математику

Рис. 151

19.26.Достаточно перегнуть кусок материи пополам, затем одну из половинок перегнуть еще раз пополам и, наконец, ту четвертинку, которая ближе к середине, снова перегнуть пополам. Последняя линия сгиба разделит длину куска в отношении 3:5.

19.27.После стирки от 1 м (длины) материи останется 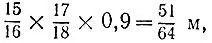поэтому нужно купить 64 м материи.

19.28.Оставшийся после стирки кусок составляет 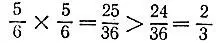первоначального объема. Поэтому его хватит еще на 2 стирки.

19.29.Оба языка знают 50% жителей, поскольку из 80% знающих английских язык 30% не знают французского языка (предполагается, что каждый житель знает хотя бы один из двух названных языков).

19.30.Новые цены составляют 4/ 5 старых; следовательно, товаров на отведенную сумму можно купить в 5/ 4 раза, т. е. на 25%, больше.

19.31.Так как для искомой суммы х рублей справедливо неравенство х + 0,02х ≤ 100, то 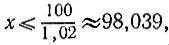а значит, имея 100 рублей, можно перевести максимум 98 рублей 3 копейки.

19.32.Выгоднее купить большой арбуз, так как его объем в 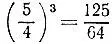раза (т. е. почти в два, а не в полтора) больше, чем объем другого арбуза.

19.33.Выгоднее покупать крупные мандарины, поскольку при увеличении радиуса мандарина площадь его поверхности (пропорциональная квадрату радиуса) увеличивается не так значительно, как его объем (пропорциональный кубу радиуса).

19.34.Площадь поверхности у одного килограмма крупной картошки меньше, чем у того же количества мелкой. Поэтому крупную картошку чистить выгоднее: и быстрее и экономнее (меньше отходов).

19.35.Было отпито 7/ 8 исходного количества сока, так как из соображений подобия объем оставшейся части сока составляет 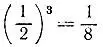прежнего.

19.36.Широкая кружка более вместительна, так как площадь ее основания в 1,5 2= 2,25 раза больше площади основания другой кружки, а объем соответственно больше в 2,25/ 2= 1,125 раза.

19.37.Будем наклонять кружку в точности до тех пор, пока не появится краешек дна (рис. 152). Тогда в кружке останется ровно полкружки молока.

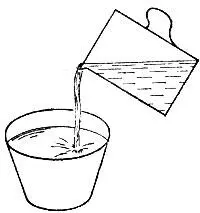
Рис. 152

19.38.Во-первых, из полной кюветы можно отлить ровно половину (рис. 153).

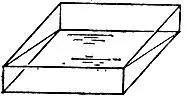
Рис. 153

Во-вторых, можно отлить из кюветы столько воды, чтобы осталась ровно шестая часть кюветы (рис. 154).

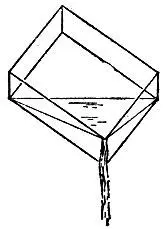
Рис. 154

В-третьих, при наличии какого-либо сосуда для временного хранения воды можно комбинировать также и другие порции воды, кратные шестой части кюветы:

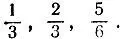
19.39.Измеряем диаметр d основания (внутренний, с учетом толщины стекла) и высоту h 1столба жидкости, а

затем перевертываем бутылку горлышком вниз и измеряем высоту h 2столба воздуха в бутылке рис. 155. Теперь остается произвести подсчет

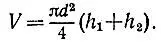
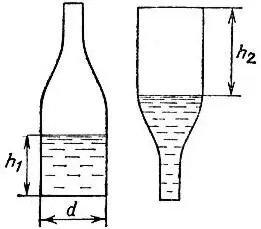
Рис. 155

19.40.Опустим предмет, например, в банку и нальем в нее воды так, чтобы предмет был полностью покрыт водой. Затем, вынув предмет из банки, измерим, на сколько понизится при этом уровень воды. Объем предмета будет равен произведению полученной величины на площадь сечения банки.

19.41.Достаточно поделить объем израсходованной краски на площадь окрашенной поверхности.

19.42.Это можно сделать за четыре операции, результаты которых указаны в следующей таблице (сами операции без труда угадываются по данным таблицы):

19.43.Для выполнения поставленной задачи необходимо сделать минимум 9 переливаний, результаты которых оформлены в виде следующей таблицы:

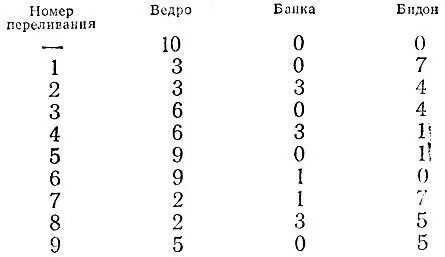
19.44.Достаточно четырех взвешиваний. Сначала взвешиваем 1 кг песку, затем еще 2 кг (положив на одну чашку весов уже взвешенный песок и гирю), затем еще 3 кг (сложив на одной чашке 1 + 2 = 3 кг взвешенного песка) и, наконец, еще 7 кг (сложив на одной чашке весь песок и гирю). Меньшим числом взвешиваниями обойтись нельзя, так как за три взвешивания можно набрать максимум 1 + 2 + 4 = 7 кг песку.

19.45.Если гири можно класть только на одну чашку весов, то необходимо иметь, как минимум, четыре гири. Годится, например, набор гирь в 1, 2, 4, 8 кг. Если же разрешить класть гири на обе чашки, то необходимо иметь три гири. Так, из трех гирь в 1, 3, 9 кг можно скомбинировать любой вес от 1 до 13 кг .

19.46.Для того чтобы взвесить мелкий предмет на грубых весах, нужно увеличить вес этого предмета в достаточное число раз. В нашем случае можно взвесить, скажем, 100 монет по 1 копейке, а затем полученный вес поделить на 100. Полезно знать, однако, что вес копейки равен 1 г.

19.47. а) Три предмета можно упорядочить тремя сравнениями: каждый предмет сравнить с каждым.

б) Для четырех предметов достаточно пяти сравнений: тремя сравнениями упорядочиваются некоторые три предмета, а затем со средним из них сравнивается четвертый предмет, который в зависимости от результата сравнивается, наконец, с одним из двух оставшихся предметов тройки.

в) Пять предметов можно упорядочить семью сравнениями: сначала упорядочим предметы в некоторых двух парах и сравним два более тяжелых предмета по одному из каждой пары, в образовавшуюся при этом тройку вставим пятый предмет, а затем и более легкий предмет оставшейся пары. На все это уйдет не более семи сравнений. Шести сравнений будет, вообще говоря, недостаточно.