Сергей Гашков - Примени математику

19.89.Если мысленно разрезать данный ящик на два ящика размером 20*15*9 и 20*15*5 , то в каждом из них одно измерение будет делиться на 10, другое на 5 и еще одно на 3. Поэтому оба ящика, а значит, и исходный можно заполнить коробками.

19.90.Можно разместить 68 кругов так, как изображено на рис. 174. При этом останется неиспользованной полоска шириной

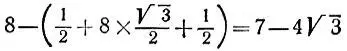
(последняя величина положительная, поскольку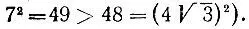

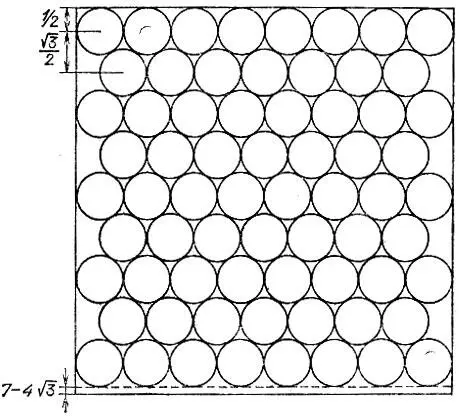
Рис. 174

19.91.Если бы это было возможно, то в круге радиуса 550 м можно было бы разместить без наложений 125 кружков радиуса 50 м каждый с центрами в скважинах. Но тогда общая площадь этих кружков, равная 125*2500*π м 2 была бы меньше площади объемлющего круга, равной 550*550π м 2 , что не соответствует истине. Значит, указанное размещение скважин невозможно.

19.92.Если данная точка С не принадлежит окружности, то найдем точки D и Е пересечения прямых АС и ВС с окружностью, а затем точку F пересечения прямых АЕ и BD (рис. 175). Тогда прямая CF представляет собой искомый перпендикуляр.

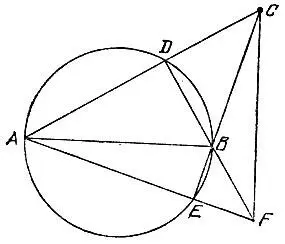
Рис. 175

Если же точка С лежит на окружности, то проведем какой-либо перпендикуляр к диаметру АВ, пересекающий окружность в точках К и L (рис. 176), а затем найдем точки М и N пересечения прямой CL с диаметром АВ и прямой КМ с окружностью соответственно. Тогда прямая CN будет также перпендикулярна диаметру.

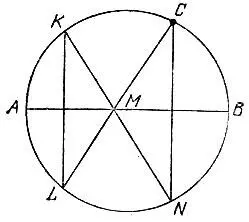
Рис. 176

19.93.Проведя на одинаковых расстояниях (равных ширине h линейки) от сторон данного угла параллельные прямые (рис. 177), мы получим ромб, диагональ которого делит угол пополам.

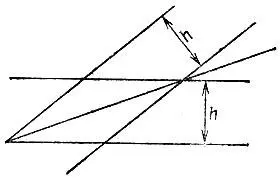
Рис. 177

19.94.Проведем по одинаковому количеству прямых, параллельных обеим сторонам угла, на расстояниях, кратных ширине h линейки. Соответствующие точки пересечения этих прямых лежат на биссектрисе угла (рис. 178).

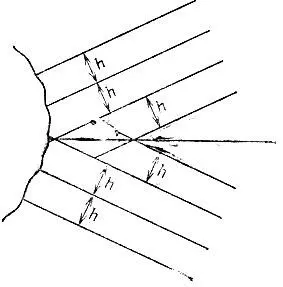
Рис. 178

19.95.Проведем прямую, параллельную данному отрезку АВ, и построим треугольник АСВ, стороны АС и ВС которого пересекают прямую в точках D и Е (рис. 179). Тогда, проведя через точку F пересечения прямых АЕ и BD прямую CG, мы разделим отрезок АВ пополам.

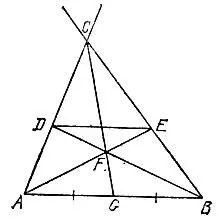
Рис. 179

19.96.Используя конструкцию, описанную в решении задачи 19.95, построим два равнобедренных треугольника A 1С 1B 1 и А 2С 2В 2 (рис. 180) и проведем их медианы, на пересечении которых как раз и будет лежать центр окружности.

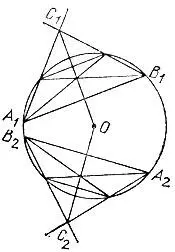
Рис. 180

19.97.Отложив на данной прямой две точки на расстоянии друг от друга, большем ширины h линейки, приложим двустороннюю линейку так, чтобы оба раза отмеченные точки примыкали к разным сторонам линейки (рис. 181). Проведя четыре соответствующие прямые, получим в пересечении ромб с одной диагональю, лежащей на данной прямой, и с другой диагональю, ей перпендикулярной.

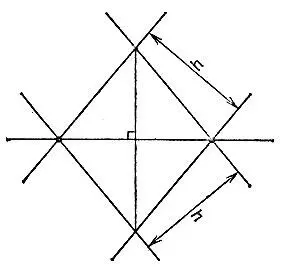
Рис. 181

19.98.Отложим на сторонах угла от его вершины по два отрезка длиной 1 см каждый (см. задачу 9.7 и рис. 10). Соединив четыре полученные точки попарно крест-накрест, мы получим точку биссектрисы (рис. 182).

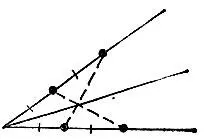
Рис. 182

19.99.Впишем в данную окружность два прямых угла, которые будут опираться на диаметры (рис. 183). Тогда точка пересечения этих диаметров укажет центр окружности.

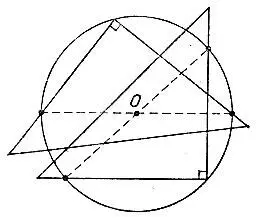
Рис. 183

19.100.Построим два прямоугольника с общей стороной, совпадающей с данным отрезком. Тогда, соединив друг с другом точки пересечения их диагоналей, мы найдем середину этого отрезка (рис. 184).

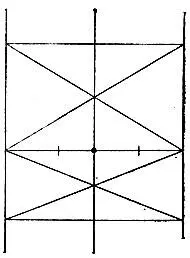
Рис. 184

19.101.Можно сильно приблизить друг к другу вершины исходного прямоугольника, перенеся каждую из них вдоль длинной стороны к ее середине на ширину шоколадки (рис. 185).

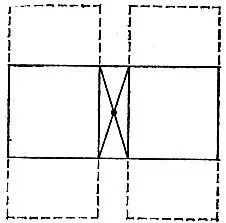
Рис. 185

19.102.Проведем какую-либо дугу с центром в данной точке А, чтобы получились две точки В и С пересечения с исходной дугой (рис. 186). Затем найдем точку D, отличную от точки А и равноудаленную от точек В к С. Прямая AD будет искомой.

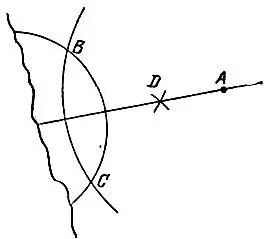
Рис. 186

19.103.Построим точку С на равном расстоянии от точек А и В и отложим на луче ВС точку В на том же расстоянии от точки С (рис. 187). Тогда угол BAD будет прямым.

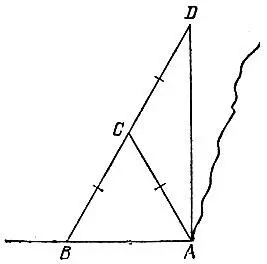
Рис. 187

19.104.Положим бумагу на цилиндрический предмет, например на трубу, и, установив одну ножку циркуля на полученной поверхности, проведем на ней циркулем "окружность" (рис. 188). Распрямив затем лист, получим на нем кривую овальной формы.

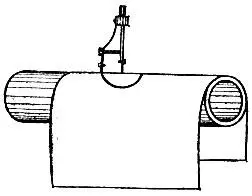
Рис. 188

19.105.Точки А, В, С, D (первые две точки считаем данными) на рис. 189 лежат на одной прямой, при этом все дуги одинакового радиуса АВ проводятся последовательно с центрами в В, А, Е, F, С, G.

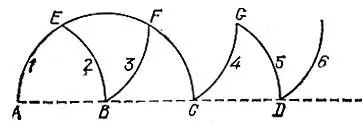
Рис. 189

19.106.По данным концам отрезка А В построим точку С так, как указано в решении задачи 19.105. Затем проведем дугу 2 с центром С и радиусом АС. Наконец, проведем дугу 3 с центром D (рис. 190) и радиусом AD, которая пересечет отрезок АВ в его середине М (если даже отрезок АВ, как таковой, не проведен, точку М можно построить, проведя дополнительно дугу 4 с центром Е).