Сергей Гашков - Примени математику

И. Н. Сергеев

С. Н. Олехник

С. Б. Гашков

Москва "Наука"

Главная редакция физико-математической литературы

1989

ББК 22.1

С 32

УДК 51(023)

Рецензент

доктор физико-математических наук В. Г. Демин

Сергеев И. Н., Олехник С. Н., Гашков С. Б.

С 32Примени математику.- М.: Наука. Гл. ред. физ.-мат. лит., 1989.- 240 с.

ISBN 5-02-013946-7

На примере решения большого числа конкретных задач в основном практического содержания показывается, как использовать математические идеи и методы для нахождения выхода из разного рода затруднительных положений, которые могут возникнуть в повседневной жизни. Рассматриваются вопросы построения и измерения ограниченными средствами, поиска оптимального решения в той или иной ситуации, способы быстрого счета, задачи на разрезание, переливание, взвешивание и т. п.

Для школьников и всех любителей математики.

ББК 22.1

При написании этой книги мы ставили своей целью научить читателя искусству применения математических идей и методов к решению практических и теоретических задач, к нахождению выходов из разного рода затруднительных положений, возникающих в повседневной жизни, и даже к тем вопросам, в которых использование математики поначалу кажется просто невозможным.

Книга представляет собой сборник задач, сгруппированных по темам в отдельные параграфы. В связи с этим принята двойная нумерация задач. Например, задача 14.6 содержится в § 14 и идет там шестой по счету. В начале каждого параграфа приводятся необходимые сведения, соглашения и понятия, используемые в задачах. Решения задач помещены в конце соответствующих параграфов. В пределах одного параграфа задачи расположены в основном по возрастанию трудности. Рекомендуем решать их по порядку и сравнивать полученные решения с приведенными в книге.

Некоторые задачи этого сборника заимствованы из различных занимательных математических книг и журналов. При этом отбирались наиболее интересные и поучительные на наш взгляд задачи, имеющие практическое значение. Многие задачи переработаны нами или придуманы специально для этой книги. Мы старались приводить наиболее простые из известных нам и легко осуществимые на практике решения, доступные по возможности более широкому кругу читателей. Однако вполне допускаем, что какие-то из приведенных решений окажутся не самыми лучшими,

В книге нет громоздких формул, сложных выкладок или заумных рассуждений. Для решения задач не требуются ни толстые справочники, ни сверхточные приборы, ни быстродействующие компьютеры - нужны лишь карандаш, листок бумаги и, главное, ... смекалка, Надеемся, что задачи доставят читателю немалое удовольствие, А если ему удастся впоследствии на деле применить приобретенные знания, то он, возможно, испытает радость и от неожиданного практического их эффекта. Итак, за работу!

Авторы

Многим из вас когда-нибудь приходилось и, скорее всего, еще не раз придется заниматься различными вычислениями. Вы, наверняка, заметили, что считать "вручную" на бумаге или тем более в уме - дело кропотливое и к тому же весьма ненадежное. Ведь любая ошибка (а при большом объеме вычислений с возможностью сделать ошибку нельзя не считаться) ведет к неверному ответу, проверка которого означает пересмотр всех сделанных выкладок. Если же в результате этого пересмотра ответ не совпадает с первоначальным, то возникает вопрос, какому из двух ответов больше доверять. Стало быть, нужно набраться терпения и пересчитать все заново, а возможно, и не один раз.

Между тем бороться с указанными неприятностями можно. Один из способов вам хорошо известен - это использование калькуляторов. К сожалению, калькулятор не всегда имеется под рукой. Поэтому полезно уметь немножко разнообразить скучное занятие, связанное с вычислениями, используя различные приемы как для упрощения выкладок, так и для их проверки. В настоящем параграфе вы найдете подборку задач, в которых как раз и разрабатываются такие приемы.

1.1. Сумма цифрТребуется сложить много однозначных чисел. Как облегчить эту работу и быстрее получить правильный ответ?

1.2. Сложение большого количества двузначных чиселПроделайте следующий эксперимент: откройте книгу на произвольной странице дальше 10-й и запишите число, составленное из двух последних цифр номера страницы. Открывая книгу много раз (скажем, ?0) и беря числа попеременно то с правой, то с левой стороны книги, вы получите большой набор двузначных чисел. Попробуйте быстро найти их сумму.

Какие приемы позволяют упростить эту работу?

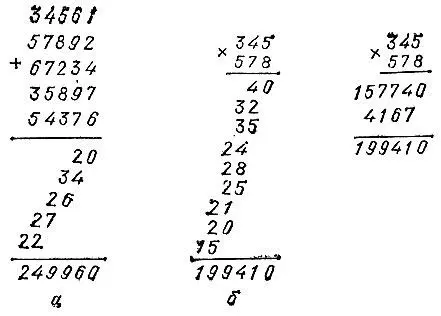
1.3. Необычные записи

Рис. 1

На рис. 1 приведены любопытные способы записи операций сложения и умножения многозначных чисел. Разберитесь в этих способах.

1.4. Таблица умножения на пальцахЕсли вы хорошо знаете таблицу умножения чисел, меньших 5, но почему-то неуверенно себя чувствуете при умножении однозначных чисел, больших 5, то вы можете контролировать себя с помощью пальцев следующим образом. Пусть надо перемножить числа 6 и 7. Загнем на одной руке столько пальцев, на сколько первый сомножитель превышает 5 (в нашем случае 6-5 = 1 палец), а на другой руке столько пальцев, на сколько второй сомножитель превышает 5 (в нашем случае 7-5 = 2 пальца). Если сложить количества загнутых пальцев и перемножить количества незагнутых пальцев, то получится соответственно число десятков 1+2 = 3 и число единиц 4*3 = 12 , а сумма 30 + 12 = 42 как раз и будет равна произведению 6*7 .

Дайте обоснование предложенному способу умножения;

1.5. Умножение на 9 с помощью пальцевЭтот способ настолько прост, что его может освоить любой ребенок, знакомый лишь с элементарным счетом. Пусть нужно умножить 6 на 9. Положив обе руки на стол, приподнимем шестой палец, считая слева направо. Тогда количество пальцев слева от поднятого укажет цифру десятков (в нашем случае 5), а количество пальцев справа от поднятого укажет цифру единиц (равную 4), т, е. искомое произведение будет равно 54.