Сергей Гашков - Примени математику
- Название:Примени математику
- Автор:
- Жанр:
- Издательство:Наука
- Год:1989
- Город:Москва
- ISBN:5-02-013946-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Сергей Гашков - Примени математику краткое содержание
Рассматриваются вопросы построения и изменения ограниченными средствами, поиска оптимального решения в той или иной ситуации, способы быстрого счета, задачи на разрезание, переливание, взвешивание и т. п.
Для школьников и всех любителей математики.
Источник:
Примени математику - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
2.12.Описанная в задаче проверка умножения основана на том, что если при подсчете произведения нескольких чисел не было сделано ошибки, то это произведение должно давать тот же остаток при делении на m (в задаче взято m = 9), что и произведение остатков от деления сомножителей на m. Проверка деления числа а на число b, в результате которого получены частное q и остаток r, сводится к проверке равенства
a = qb + r,
т. е. двух операций сразу: умножения и сложения. Это можно сделать, сравнив остатки от деления на m числа а и числа qb + r , в котором каждое из чисел q, b и r можно заменить остатком от деления на m. Если остатки не совпадут, то в вычислениях имеется ошибка.
2.13.Совпадение остатков от деления двух чисел на 9 не дает возможности утверждать равенство самих этих чисел: например, числа 49 и 40 имеют одинаковые остатки, но не совпадают друг с другом. Поэтому описанные в задачах 2.11 и 2.12 способы проверки вычислений не могут дать гарантии от ошибок. Та же пара чисел показывает, что даже в случае правильности всех цифр ответа, кроме, быть может, одной, этих проверок, вообще говоря, не достаточно (исключение составляет случай, когда в ответе нет ни одной цифры 0 и 9, поскольку тогда любое изменение одной цифры ответа влечет за собой изменение его остатка от деления на 9).
2.14.Если бы линейка стоила на 1 копейку дешевле, то общая стоимость товаров, выраженная в копейках, была бы кратна 4, так как в этом случае стоимость каждого вида перечисленных в условии предметов делилась бы на 4. Поскольку названа сумма 5 рублей 27 копеек, то число 27 - 1 = 26 должно делиться на 4 (см. задачу 2.5), что неверно. Таким образом, сумма подсчитана с ошибкой.
2.15.Представим данные числа в виде 6 = 2*3, 12 = 4*3, 15 = 3*5, 18 = 2*9, 24 = 8*3, 36 = 4*9, 45 = 9*5 и воспользуемся следующим утверждением: делимость на число m = pq , представляющее собой произведение взаимно простых чисел р и q, равносильна одновременной делимости на р и на q. Взаимная простота чисел р и q играет существенную роль, поскольку без этого требования утверждение было бы неверно. Например, несмотря на справедливость разложения 24 = 4*6 , из делимости числа 12 на 4 и на 6 не следует его делимость на 24. В то же время делимость какого-либо числа на 8 и на 3 влечет за собой его делимость на 24.
2.16.Пусть q 1, q 2, q 3, ... - частные от деления на m чисел 10 1, 10 2, 10 3, ... соответственно с остатками m 1, m 2, m 3, ... Тогда справедливо представление
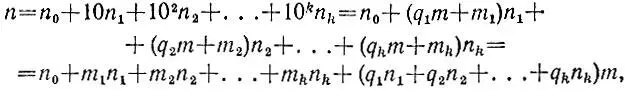
из которого следует, что числа n и
f m(n)= n 0+m 1n 1+m 2n 2+. ..+m kn k
дают одинаковые остатки при делении на m. Кроме того, если при последовательном вычислении остатков m 1, m 2, m 3, ... уже найден остаток m k, то остаток от деления на m числа
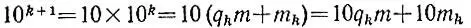
равен остатку от деления на m слагаемого 10m k в последней сумме.
2.17.Полагая в признаке Паскаля m = 2, m = 3, m = 5 и m = 9, получаем для (k+1) -значного числа п следующие числа:
f 2(n)= n 0 ,
f 3(n)= n 0+n 1+n 2+. ..+n k ,
f 5(n)= n 0 ,
f 9(n)= n 0+n 1+n 2+. ..+n k .
Эти числа определяют в точности те же признаки делимости, что и сформулированные в задачах 2.4, 2.8, 2.1, 2.9.
2.18.Полагая в признаке Паскаля m = 4 и m = 8 , получаем для k-значного числа n следующие числа:
f 4(n)= n 0+2n 1, f 8(n)= n 0+2n 1+4n 2 .
Получаемые в результате признаки делимости на 4 и на 8 несколько отличаются от приведенных в задачах 2.5 и 2.6, однако вряд ли могут рассматриваться как более простые, поскольку, на наш взгляд, требуют чуть больше вычислений.
2.19.Доказательство модификации признака Паскаля, по существу, ничем не отличается от доказательства, приведенного в решении задачи 2.16. Разница состоит лишь в том, что деление каких-то из чисел 10 1, 10 2, 10 3, ... на m нужно провести не с остатком, а с недостатком, т. е. в соответствующих формулах
10 k= q km + m k
положительные числа m kвзять на m меньшими прежних (отрицательными), a q k- на 1 большими прежних.
2.20.Производя в признаке Паскаля деление степеней десятки на 11 попеременно то с остатком, то с недостатком, имеем
10 = 11 - 1, m 1= -1,
10m 1= -10 = -11 + 1, m 2= 1,
10m 2= 10 = 11 - 1, m 3= 1,
откуда получаем, что число 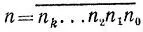 дает тот же остаток при делении на 11, что и число
дает тот же остаток при делении на 11, что и число
f 11(n)= n 0-n 1+n 2-n 3+. ..+(-1) kn k .
Поэтому для делимости числа n на 11 необходимо и достаточно, чтобы суммы n 0+ n 2+ ... и n 1+ n 3+ ... отличались друг от друга на число, кратное 11.
2.21.Подставляя значение m = 11 в утверждения, сформулированные в решениях задач 2.11 и 2.12, и используя признак делимости на 11, получаем способы проверки сложения и умножения. Если у числа n, представляющего собой истинный ответ, заменить одну цифру на неверную, то число f 11(n) обязательно изменится на некоторое число, меньшее 11 (даже меньшее 10), а значит, будет давать другой, уже неверный остаток от деления на 11. Поэтому, сравнив его с верным остатком, можно обнаружить ошибку. Более того, если известно, в какой именно цифре числа n возможна-ошибка, эту цифру можно однозначно восстановить.
2.22.Действуя согласно модифицированному признаку Паскаля, при m = 7 имеем
10 = 7 + 3, m 1= 3,
10 m 1= 30 = 28 + 2, m 2= 2,
10 m 2= 20 = 21 - 1, m 3= -1,
10 m 3= -10 = -7 -3, m 4= -3,
10 m 4= -30 = -28 - 2, m 5= -2,
10 m 5= -20 = -21 + 1, m 6= 1,
10 m 6= 10 = 7 + 3, m 7= 3, ... ,
откуда получаем, что число 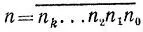 дает тот же остаток при делении на 7, что и число
дает тот же остаток при делении на 7, что и число
f 7(n) = n 0+ 3n 1+ 2n 2- (n 3+ 3n 4+ 2n 5)+...
2.23.Пусть все цифры числа n разбиты на тройки, образующие трехзначные числа n 0, n 1, n 2, ..., n k (начиная справа). Тогда число
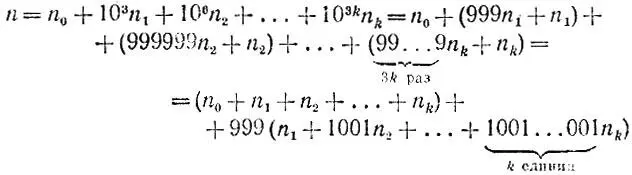
дает при делении на 37 тот же остаток, что и сумма n 0+ n 1+ n 2+ ... + n k , поскольку в полученном представлении числа n второе выражение делится на 999 = 37*27. Если указанная сумма является более чем трехзначным числом, то к ней можно применить те же рассуждения, что и к исходному числу n, и этот процесс можно продолжать до тех пор, пока не получится трехзначное число. Наконец, любое трехзначное число 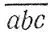 сводится к двузначному переходом к разности чисел
сводится к двузначному переходом к разности чисел 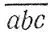 и
и 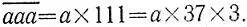
Интервал:
Закладка:










