Сергей Гашков - Примени математику

3.6. Корень кубический в умеВозведите в куб каждое из чисел 0, 1, 2, ..., 9 и придумайте способ быстрого извлечения корня кубического из данного целого числа, имеющего в десятичной записи не более шести знаков, в предположении, что этот корень извлекается из данного числа нацело. Найдите корни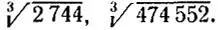

3.7. Корень квадратный в умеКаким способом можно быстро извлечь корень квадратный из целого числа, имеющего в десятичной записи не более четырех знаков, в предположении, что этот корень извлекается из данного числа нацело?

Найдите корни 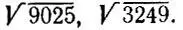Попробуйте найти корень наиболее простым способом.

3.8. По остатку от деления на 11Укажите, как по остатку от деления на 11 куба целого числа можно найти остаток от деления на 11 самого числа. Пользуясь признаком делимости на 11, придумайте способ быстрого извлечения корня кубического из данного целого числа, имеющего в десятичной записи от семи до девяти знаков, в предположении, что этот корень извлекается нацело. Найдите корень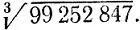

3.9. Алгоритм извлечения корня квадратногоДля нахождения корня 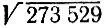произведем следующие действия (см. рис. 2):

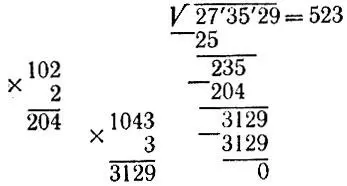
Рис. 2

а) десятичную запись числа 273 529 разобьем на группы по две цифры (как в решении задачи 3.1);

б) для старшей группы цифр, образующей число 27, подберем такую цифру, чтобы ее квадрат был наибольшим, но не превосходил числа 27; такой цифрой будет 5, ее и запишем в качестве первой цифры ответа;

в) из старшей группы цифр вычтем найденный в предыдущем пункте квадрат первой цифры ответа и к полученной разности (остатку) 27 - 25 = 2 припишем справа (снесем) следующую группу цифр 35; получим число 235;

г) удвоив записанное в ответе число 5, припишем справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходило числа 235; такой цифрой будет 2 (ибо 102*2 = 204≤235, но 103*3 = 309>235), ее и запишем в качестве второй цифры ответа;

д) из числа 235 вычтем найденное в предыдущем пункте произведение 204 и к остатку 31 снесем следующую группу цифр 29; получим число 3129;

е) удвоив записанное в ответе число 52, припишем справа такую цифру, чтобы произведение полученного в результате числа на эту цифру было наибольшим, но не превосходило числа 3129; такой цифрой будет 3 (ибо 1043*3 = 3129), ее и запишем в качестве третьей цифры ответа;

ж) разность между снесенным числом 3129 и полученным в предыдущем пункте произведением равна 0, поэтому корень квадратный из числа 273 529 извлекается нацело и равен записанному в ответе числу 523.

Приведите обоснование предложенному алгоритму и найдите с его помощью корень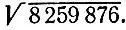

3.10. Где остановиться?Объясните, как следует поступать в случае, если предложенный в задаче 3.9 алгоритм в применении к данному числу не заканчивается ни на каком шаге, т. е. не наступает ситуация, описанная в п. ж) задачи 3.9. Докажите, что предложенный алгоритм позволяет и в этом случае находить значение корня квадратного с любой наперед заданной точностью. Найдите приближенное значение 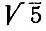с точностью до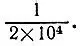

3.11. Приближенная формула корня квадратногоНайдя какое-нибудь, пусть даже совсем грубое, приближенное значение х>0 корня квадратного из данного числа а = х 2+ b, мы можем значительно улучшить приближение с помощью формулы

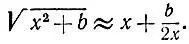
Докажите, что погрешность 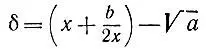полученного приближения будет удовлетворять оценкам

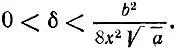
Какое значение для 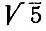даст приведенная формула, если в качестве грубого приближения взять целую часть этого корня, а именно число х = 2 ?

3.12. Способ ГеронаВыберем какое-либо приближение х 0корня квадратного из данного числа а (например, х 0= а ) и будем последовательно улучшать приближения по формулам

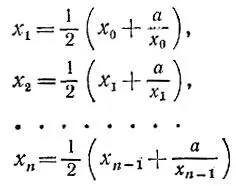
и т. д. Докажите, что погрешности 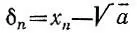(для приближений 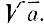числами последовательности х n) удовлетворяют оценкам

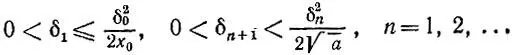
Проверьте, что этот способ сводится к многократному применению приближенной формулы корня квадратного (см. задачу 3.11). Найдите с помощью способа Герона приближенное значение 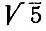, взяв х 0= 2 и проделав два шага. Оцените точность найденного приближения.

3.13. Почти удвоение точностиПусть после вычисления первых n значащих цифр корня квадратного из данного числа а (например, с помощью алгоритма задачи 3.9) в ответе получилось приближенное значение х и остаток b = а - х 2 . Объясните, почему приближение 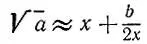задает в дополнение к п первым знакам еще по меньшей мере n-1 верных знаков корня. Пользуясь вычислениями задачи 3.10, найдите приближенное значение 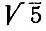с точностью до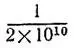

3.14. Приближенная формула корня кубическогоНайдя какое-нибудь приближение x>0 корня кубического из данного числа а = х 2+ b , можно значительно улучшить приближение с помощью формулы

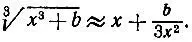
Оцените при b>0 погрешность 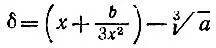полученного приближения, рассмотрев отдельно случай, когда число х представляет собой целую часть искомого корня. Найдите приближенное значение 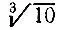по указанной формуле, оценив погрешность.