Сергей Гашков - Примени математику

3.7.В отличие от случаев с нечетными степенями, рассмотренных в задачах 3.5 и 3.6, последняя цифра целого числа, вообще говоря, не восстанавливается однозначно по последней цифре его квадрата. Действительно, одинаковыми цифрами оканчиваются квадраты чисел, взаимно дополняющих друг друга до 10:

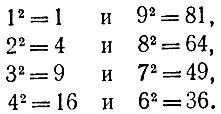
Но "индивидуальными" цифрами оканчиваются квадраты 0 2= 0, 5 2= 25. Таким образом, последняя цифра числа предположении, что это число целое, равна 5, а первая равна 9, так как

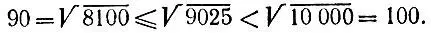
Поэтому искомый корень может быть равен только 95, что и оказывается верным.

Менее простым для вычисления является корень квадратный из числа 3249. Первая цифра этого корня равна 5, так как 5 2= 25≤32<36 = 6 2 , а вторая, если искомое число целое, равна либо 3, либо 7, т. е. вторая цифра либо меньше 5, либо больше 5. Но это можно проверить, сравнив число 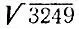с числом 55. Из оценки (см. задачу 1.17)

55 2= 5*6*100 + 25 = 3025<3249вытекает, что искомый корень больше 55, а значит, равен 57, что подтверждается проверкой.

Для нахождения числа 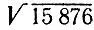в предположении, что оно целое, определим первые две его цифры из неравенств

12 2= 144≤158<169 = 13 2.Итак, искомый корень трехзначен, начинается цифрами 1, 2, а кончается либо цифрой 4, либо цифрой 6. Так как этот корень больше числа 125, что следует из оценки

125 2= 12*13*100 + 25 = 15 625<15 876,то он равен 126.

3.8.Подсчет показывает (см. решение задачи 3.6), что остатки от деления на 11 кубов целых чисел от 0 до 10 равны соответственно 0, 1, 8, 5, 9, 4, 7, 2, 6, 3, 10. Анализ этих остатков показывает, что все они различны и по ним однозначно восстанавливаются соответствующие основания кубов. Поэтому, зная остаток от деления на 11 данного числа, из которого нацело извлекается корень кубический, можно определить остаток от деления на 11 этого корня. Если мы знаем первую и последнюю цифры трехзначного корня кубического (а именно таким он должен оказаться в условиях задачи), то средняя цифра этого корня определяется остатком от его деления на 11.

Например, методами задачи 3.6 вычисляются первая цифра 4 и последняя цифра 3 корня кубического из числа 99 252 847. Сосчитав остаток от деления исходного числа на 11, равный остатку от деления на 11 выражения

7 - 4 + 8 - 2 + 5 - 2 + 9 - 9 = 12(см. признак делимости - задачу 2.20), т. е. равный числу 1, заключаем, что остаток от деления на 11 искомого корня равен 1. После этого из условия, что число 4*3, ас ним и число 3 - x + 4 = 7 - х , должно давать при делении на 11 остаток 1, мы однозначно определяем среднюю цифру х = 6 корня и в конечном счете сам корень 463. Остается лишь убедиться в том, что он действительно удовлетворяет равенству 463 3= 99 252 847.

3.9.Предложенный алгоритм в разобранном случае базируется на представлении

273 529 = 5*5*10 000 + (2*5*10 + 2)*2*100 + (2*52*10 + 3)*3 = 500*500 + (2*500 + 20)*20 + (2*520 + 3)*3 = 500 2+ 2*500*20 + 20 2+ 2*520*3 + 32 = (500 + 20 + 3) 2,из которого вытекает равенство 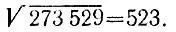В общем же случае алгоритм позволяет представить данное число, являющееся квадратом целого числа, в виде

где числа а 1, a 2, ..., a n выбираются максимально возможными, кратными соответствующим степеням десяти: 10 n-1, 10 n-2, ..., 10 0 , т. е. указывают цифры в соответствующих разрядах десятичной записи корня.

Нахождение корня 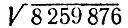по этому алгоритму записывается так:

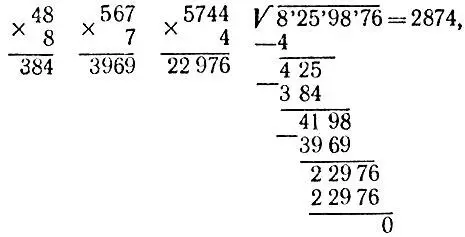
откуда следует, что искомый корень равен 2874.

3.10.Согласно утверждению задачи 3.3, можно без ограничения общности считать число, из которого требуется извлечь корень, целым и даже сколь угодно большим (если оно положительно), т. е. имеющим больше пар цифр, чем нужно получить знаков в десятичной записи корня. Этого можно достичь временным домножением числа на правильно подобранную четную степень числа 10 и последующим делением значения корня на вдвое меньшую степень числа 10. Если на последнем шагу получается ненулевой остаток, то можно оборвать алгоритм и считать получившийся при этом ответ приближенным значением корня с недостатком (на каждом шагу цифры ответа выбираются максимально возможными, поэтому любая десятичная дробь, превышающая полученную в ответе хотя бы по одному из ее найденных разрядов, будет больше искомого корня). Округлив полученную дробь до предпоследнего разряда, мы найдем нужное число точных знаков корня.

Для нахождения значения 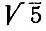с точностью до 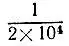произведем следующие действия:

из которых получаем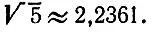

3.11.Так как

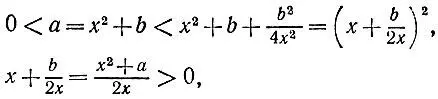
то 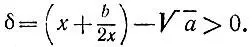Возводя в квадрат обе части равенства

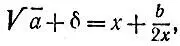
получаем 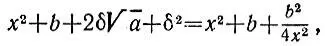откуда имеем

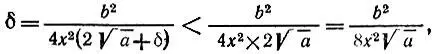
что и требовалось доказать.

Для 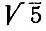приближенная формула дает значение 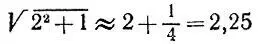с точностью до 1/ 64.

3.12.Из преобразований

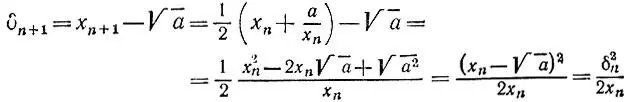
при n = 0 получаем первую из требуемых оценок, а при n = 1, 2, ... имеем, что число δ nположительно, следовательно, 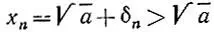и