Сергей Гашков - Примени математику

479, 481, 487, 491, 499, 509.

Одна из простейших задач, для решения некоторой понадобится найти наибольший общий делитель пары натуральных чисел а и b,- это 1 задача сокращения дроби a/ b. Напомним, что если числа а и b делятся на одно и то же натуральное число d, то число d называется общим делителем пары чисел а и b. Любая пара натуральных чисел имеет хотя бы один общий делитель (а именно, d = 1), причем любой общий делитель не превосходит каждого из этих чисел. Поэтому среди всех делителей чисел а и b можно выбрать наибольший общий делитель, который обозначается через (а, b), например (20, 100) = 20, (65, 39) = 13. Если (а, b) = 1, то числа а и b называются взаимно простыми.При этом взаимно простые числа а и b совсем не обязательно сами по себе должны быть простыми числами; так, (33, 35) = 1, но 33 = 3*11 и 35 = 5*7.

У читателя, возможно, сложилось впечатление, что нахождение наибольшего общего делителя пары чисел представляет собой очень простую задачу. Ведь если разложить на простые множители каждое из данных чисел, то сразу станет ясно, как составить из этих простых множителей наибольшее произведение, на которое делятся оба данных числа. Однако все дело в том, что разложить число на простые множители иногда бывает довольно трудно, тогда как нахождение наибольшего общего делителя можно осуществить намного проще - с помощью несложной процедуры. Эта процедура известна уже более 2 тысяч лет и носит название алгоритма Евклида.

Алгоритм Евклида применяется ко многим с виду разнородным объектам. Нахождение наибольшего общего делителя, разложение дроби в цепную дробь, приближение дроби более простыми, решение уравнений в целых числах - вот далеко не полный перечень приложений этого алгоритма, с которыми вы познакомитесь в настоящем и следующем параграфах.

5.1. Разлагая на множителиНайдите наибольший общий делитель пары чисел a и b путем разложения их на простые множители:

а) а = 36, b = 20; б) а = 1365, b = 1225; в) а = 1189, b = 589.

5.2. Первый шагДокажите, что если число а при делении на b дает остаток r, то

(a, b) = (b, r),т. е. наибольший общий делитель пары чисел а и b совпадает с наибольшим общим делителем пары чисел b и r. Каким будет наибольший общий делитель пары чисел а и b, если число а делится на b нацело?

5.3. Алгоритм ЕвклидаДля нахождения наибольшего общего делителя пары натуральных чисел а 1и а 2поступают следующим образом: деля а 1на а 2, получают остаток а 3, затем, деля а 2на а 3, получают остаток а 4, затем, деля а 3на а 4, получают остаток а 5и так далее до тех пор, пока некоторое число а nне разделится на а n+1нацело. Запись этого алгоритма можно оформить так:

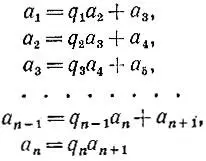
(числа q 1, q 2, ..., q n будем называть в дальнейшем последовательными частными ).

Докажите, что описанный алгоритм обязательно закончится (т. е. при некотором значении n число а nразделится на а n+1нацело), а число а n+1окажется равным наибольшему общему делителю пары чисел а 1и а 2.

5.4. Не разлагая на множителиПрименяя алгоритм Евклида, найти наибольший общий делитель пары чисел а и b, указанных в п. а), б), в) задачи 5.1.

5.5. Найдя наибольший общий делительСократите дробь: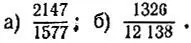

5.6. Разрезание на квадратыНа рис. 3 изображен прямоугольник размером 135*40, который разрезан на квадраты различной величины. Установите размеры квадратов и укажите связь между разрезанием на квадраты любого прямоугольника с целочисленными сторонами и алгоритмом Евклида (см. задачу 5.3).

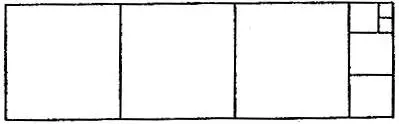
Рис. 3

5.7. Цепная дробьОдним из применений алгоритма Евклида является представление дроби a 1/ a 2в виде

где q 1- целое число, a q 2, q 3, ..., q n - натуральные числа. Такое выражение называется цепной (конечной непрерывной) дробью. Докажите, что любую дробь a 1/ a 2можно разложить в цепную дробь, в которой числа q 1, ..., q n являются последовательными частными алгоритма Евклида для нахождения наибольшего общего делителя пары чисел a 1и a 2.

5.8. Разложение в цепную дробьРазложите следующую дробь в цепную дробь:

а) 7/ 3; б) 84/ 39; в) 33/ 78.

5.9. Свертывание цепной дробиЕсли в цепной дроби (см. задачу 5.7), начиная с конца, последовательно произвести указанные в ней операции по правилам действий с дробями, то в итоге получится обыкновенная дробь, разумеется, равная исходной.

Докажите, что полученная таким образом дробь будет несократимой. На основании этого утверждения сократите дробь 155/ 93, разложив ее в цепную дробь, а затем свернув в обыкновенную.

5.10. Подходящие дробиПусть задана цепная дробь с последовательными частными q 1, q 2, ..., q n (см. задачу 5.7). Выражения

называются подходящими дробями порядка 1, 2, 3, ..., n соответственно. Разложите дробь 13/ 29в цепную дробь и выпишите все подходящие к ней дроби. Обратите каждую из подходящих дробей в обыкновенную.

5.11. Комбинирование сопротивлений

Рис. 4

Из курса физики вам, наверняка, известно, что если соединить несколько сопротивлений R 1, R 2, ..., R k в электрической цепи последовательно (рис. 4), то общее сопротивление будет равно R 1+ R 2+ ..., + R k, а если соединить эти же сопротивления параллельно (рис. 5), то общее сопротивление окажется равным

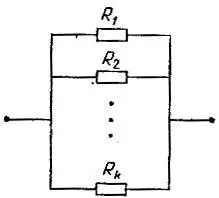
Рис. 5

А теперь представьте, что у вас есть большое количество одинаковых единичных сопротивлений. Можно ли, комбинируя их в электрической цепи специальным образом, составить схему, имеющую сопротивление:

а) 7/ 2; б) 10/ 7; в) вообще a/ b?

5.12. Кое-что о подходящих дробяхПусть для заданной цепной дроби с последовательными частными q 1, q 2, ..., q n несократимые дроби

являются результатами свертывания подходящих дробей порядка 1, 2, ..., n соответственно (см. задачу 5.10). Докажите справедливость соотношений: