Сергей Гашков - Примени математику

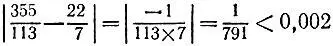
(см. соотношение п. б) задачи 5.12 при k = 3). Таким образом, шестеренки с 22 и 7 зубьями удовлетворяют всем условиям задачи.

Самые разные задачи практического содержания часто приводят к уравнениям, в которых неизвестные по своему смыслу могут принимать только целочисленные значения. Уравнения в целых числах рассматривались еще в глубокой древности. Особенно много ими занимался александрийский математик Диофант, имя которого и носят уравнения в целых числах.

Простейшим примером диофантова уравнения служит линейное уравнение

ax + by = cв целых числах (естественно, с целыми коэффициентами а, b и с). Оно может быть решено разными способами. Но, пожалуй, наиболее универсальный способ тесно связан, как это ни странно, с алгоритмом Евклида и цепными дробями (см. § 5).

6.1. Без сдачиДокажите, что любую денежную сумму, выраженную целым числом рублей, большим 7, можно уплатить без сдачи, имея лишь трехрублевые и пятирублевые купюры в достаточном количестве.

6.2. Оплата покупкиДокажите, что за любую покупку стоимостью в целое число рублей можно заплатить одними трехрублевыми купюрами, если у кассира имеются только пятирублевые купюры. Какое наименьшее количество пятирублевых купюр достаточно при этом иметь кассиру?

6.3. Необходимое условие разрешимостиПусть а, b, с - ненулевые целые числа. Докажите, что если число с не делится на наибольший общий делитель пары чисел а и b, то уравнение ах + bу = с в целых числах не имеет решений.

6.4. Сорока купюрамиМожно ли набрать сумму в 1000 рублей с помощью купюр достоинством в 1 рубль, 10 рублей, 100 рублей таким образом, чтобы всего было использовано ровно 40 купюр?

6.5. Затруднение кладовщикаНа складе имеются гвозди, упакованные в ящики по 16 кг, 17 кг и 40 кг . Может ли кладовщик отпустить 140 кг гвоздей, не вскрывая ни одного ящика?

6.6. Линейные диофантовы уравненияПокажите, как свести решение уравнения

ax + by = c

в целых числах с ненулевыми целыми коэффициентами а, b, с к решению уравнения

a'x + b'y = c'

в целых числах, коэффициенты а', b', с' которого являются натуральными числами, причем числа а' и b' взаимно просты.

6.7. Состав с углемНа станцию привезли 420 т угля в вагонах вместимостью по 15 т, по 20 т и по 25 т . Сколько каких вагонов было использовано, если известно, что всего было 27 вагонов?

6.8. Общее решениеПусть пара чисел x = x 0, y = y 0 удовлетворяет уравнению

ax + by = c

в целых числах с взаимно простыми коэффициентами а и b. Докажите, что формулы

x = x 0+ bk, y = y 0+ ak

с целым параметром k задают все решения этого уравнения,

6.9. Сколько нужно мешков?Для перевозки зерна имеются мешки, в которые входит либо 60 кг , либо 80 кг зерна. Сколько надо заготовить тех и других мешков для загрузки 1 т зерна таким образом, чтобы все мешки были полными? Какое наименьшее количество мешков при этом может понадобиться?

6.10. Сколько нужно банок?Требуется разлить 20,5 литра сока в банки по 0,7 л и 0,9 л так, чтобы все банки оказались полными. Сколько каких банок надо заготовить? Какое наименьшее количество банок при этом может понадобиться?

6.11. Частное решениеДокажите, что уравнение

ax + by = c

с взаимно простыми коэффициентами а и b имеет решение

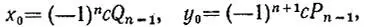
где 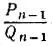- предпоследняя подходящая дробь к цепной дроби, в которую раскладывается дробь a/ b(см. задачи 5.7, 5.10, 5.12).

6.12. Загрузка трехтонокДля перевозки большого количества контейнеров по 170 кг и по 190 кг выделены трехтонные машины. Можно ли ими загружать машины полностью?

6.13. Целые точки на прямойСколько точек с целочисленными координатами, удовлетворяющими неравенствам х<0 и y>0 , лежит на прямой

8x - 13y + 11 = 0?

6.14. Наименьшим числомУ продавца имеются 100-граммовые гирьки и консервные банки весом по 450 г. Как с их помощью отвесить на чашечных весах 2,5 кг сахарного песка за один раз, используя для взвешивания наименьшее количество гирек и банок в общей сложности?

6.1.Пусть нужно уплатить денежную сумму в n рублей. Если число n делится на 3, то эту сумму можно уплатить одними трехрублевыми купюрами. Если остаток от деления числа n>7 на 3 равен 1, то

причем 3q + 1>7, откуда q>2 и, значит, в этом случае сумму можно уплатить q-3 трехрублевыми купюрами и двумя пятирублевыми. Если же остаток от деления числа n>7 на 3 равен 2, то

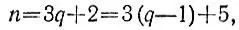
причем 3q + 2>7, откуда q>1 и, значит, в этом случае сумму можно уплатить q-1 трехрублевыми купюрами и 1 пятирублевой.

6.2.Если у кассира нет ни одной пятирублевой купюры, то покупатель может заплатить за покупку стоимостью в n рублей только при условии, что число n кратно 3. Если у кассира есть 1 пятирублевая купюра, то. покупатель может заплатить за покупку только при условии, что число n либо кратно 3, либо дает остаток 1 при делении на 3 (в последнем случае покупатель платит на 5 рублей больше и получает 5 рублей сдачи: n = 3q + 1 = 3(q + 2) - 5). Наконец, если кассир имеет 2 пятирублевые купюры, то покупатель может заплатить за покупку при любом значении n (в случае, когда остаток от деления числа n на 3 равен 2, покупатель может заплатить на 10 рублей больше и получить 10 рублей сдачи:

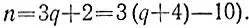
Таким образом, в условиях задачи кассир должен иметь минимум 2 пятирублевые купюры.

6.3.Пусть (a, b) = d и число с не делится на d. Тогда если уравнение ax + by = c имеет целочисленное решение x = x 0, y = y 0 , то справедливо числовое равенство ax 0+ by 0= c, в котором левая часть делится на d (ибо числа а и b кратны d), а правая нет. Полученное противоречие доказывает, что указанное уравнение в целых числах не может иметь решений.