Сергей Гашков - Примени математику

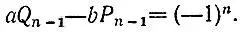
Умножая обе части последнего равенства на (-1) n, имеем

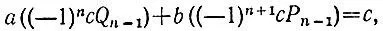
т. е. пара чисел 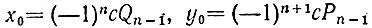является решением уравнения ax + by = с.

6.12.Обозначая через x и y количества контейнеров по 170 и 190 кг соответственно, получаем после сокращения на 10 уравнение

17x + 19y = 300

в целых неотрицательных числах. Для нахождения частного решения воспользуемся методом задачи 6.11, разложив дробь 17/ 19 в цепную дробь

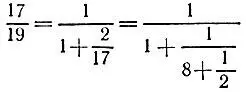
(число n получилось равным 4) и свернув предпоследнюю подходящую к ней дробь в обыкновенную

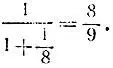
Итак, частное решение расходного уравнения имеет вид

а общее задается формулой

откуда получаем условия на параметр k

т. е. k = 142, x = 2, y = 14.

6.13.После замены переменной x' = -x (см. задачу 6.6) получаем уравнение

8x' + 13y = 11

в натуральных числах, которое решим методами, предложенными в задачах 6.8 и 6.11: предпоследняя подходящая дробь к цепной дроби

равна

откуда

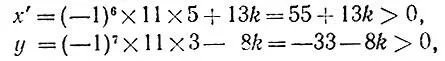
т. е. 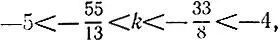что невозможно. Итак, на прямой 8x - 13y + 11 = 0 нет ни одной точки с целочисленными координатами, удовлетворяющими условиям х<0 и y>0.

6.14.Так как гирьки и банки можно класть на любую чашку весов, то числа x и y (гирек и банок соответственно) удовлетворяют уравнению

100x + 450y = 2500

в целых числах (отрицательное значение какой-либо неизвестной означает, что соответствующие предметы лежат на одной чашке с сахарным песком). Приведем уравнение к виду

2x + 9y = 50

и заметим, что числа y 0= 0, x 0= 25 дают частное решение. Поэтому общее решение имеет вид (см. задачу 6.8)

x = 25 + 9k, y = -2k.

Докажем, что наименьшее количество гирек и банок, требуемое для взвешивания, равно 8. Действительно, если гирьки и банки лежат на одной чашке весов, то x≥0, y≥0 и -3<- 25/ 9≤k≤0 , причем наименьшая сумма x + y = 25 + 7k = 11 достигается при k = -2 . Если гирьки лежат на одной чашке весов, а банки и сахар на другой, то x≥0, y≤0 и k≥0 , причем наименьшая сумма x + (-y) = 25 + 11k = 25 достигается при k = 0 . Если же банки лежат на одной чашке весов, а гирьки и сахар на другой, то x≤0, y≥0 и k≤- 25/ 9<-2 , причем наименьшая сумма (-x) + y = -25 - 11k = 8 достигается при k = -3. Таким образом, продавец должен на одну чашку весов положить 6 банок, а на другую - 2 гирьки и взвешиваемый сахар. Весы уравновесятся, если сахара будет 2,5 кг.

Важный пример диофантова уравнения дает теорема Пифагора, связывающая длины x и y катетов прямоугольного треугольника с длиной z его гипотенузы:

x 2+ y 2= z 2.

Вы, конечно, встречали одно из замечательных решений этого уравнения в натуральных числах, а именно пифагорову тройку чисел x = 3, y = 4, z = 5. Есть ли еще такие тройки?

Оказывается пифагоровых троек бесконечно много и все они давным-давно найдены. Они могут быть получены по известным формулам, о которых вы узнаете из настоящего параграфа.

Если диофантовы уравнения первой и второй степени уже решены, то вопрос о решении уравнений более высоких степеней до сих пор остается открытым, несмотря на усилия крупнейших математиков. В настоящее время, например, еще окончательно не доказана и не опровергнута знаменитая гипотеза Ферма о том, что при любом целом значении n 2 уравнение

x n+ y n= z n.

в целых числах не имеет решений.

Для решения некоторых типов диофантовых уравнений полезную роль могут сыграть так называемые комплексные числа. Что это такое? Пусть буквой i обозначен некий объект, удовлетворяющий условию i 2= -1 (понятно, что ни одно действительное число этому условию не удовлетворяет). Рассмотрим выражения вида α + iβ, где α и β - действительные числа. Такие выражения будем называть комплексными числами, определив над ними операции сложения и умножения, как и над двучленами, но с той лишь разницей, что выражение i 2 всюду будем заменять числом -1:

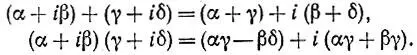
7.1. Из одной тройки многоДокажите, что если x 0, y 0, z 0 - пифагорова тройка, то тройки y 0, x 0, z 0 и x 0k, y 0k, z 0k при любом значении натурального параметра k также являются пифагоровыми.

7.2. Частные формулыПроверьте, что при любых натуральных значениях m>n тройка вида

2mn, m 2- n 2, m 2+ n 2

является пифагоровой. Всякую ли пифагорову тройку x, y, z можно представить в таком виде, если разрешить переставлять местами числа x и y в тройке?

7.3. Несократимые тройкиПифагорову тройку чисел, не имеющих общего делителя, большего 1, будем называть несократимой. Докажите, что пифагорова тройка является несократимой только в случае, если любые два из чисел тройки являются взаимно простыми.

7.4. Свойство несократимых троекДокажите, что в любой несократимой пифагоровой тройке x, y, z число z и ровно одно из чисел x или y являются нечетными.

7.5. Все несократимые тройкиДокажите, что тройка чисел x, y, z является несократимой пифагоровой тройкой тогда и только тогда, когда она с точностью до порядка первых двух чисел совпадает с тройкой 2mn, m 2- n 2, m 2+ n 2, где m>n - взаимно простые натуральные числа разной четности.

7.6. Общие формулыДокажите, что все решения уравнения

x 2+ y 2= z 2.

в натуральных числах задаются с точностью до порядка неизвестных x и y формулами