Сергей Гашков - Примени математику

Например, для заданной в задаче сократимой дроби имеем

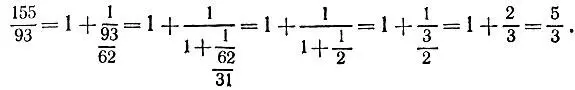
5.10.Для дроби

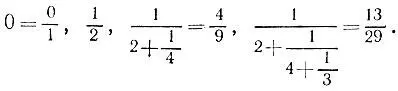
имеем следующие подходящие дроби:

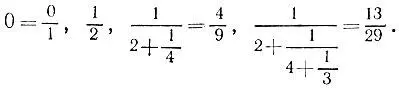
5.11.Решение этой задачи может показаться на первый взгляд совсем очевидным, поскольку для любой дроби a/ bможно сначала соединить параллельно b единичных сопротивлений, получив сопротивление, равное 1/ b, а затем размножить эту схему в а экземплярах, соединив их последовательно. При этом в конечном счете нам понадобится а*b единичных сопротивлений. Например, для такого решения п. а) их нужно 7*2 = 14 штук, а для решения п. б) -10*7 = 70 штук. Как показывает приводимое ниже решение, этот очевидный способ далеко не самый экономный: в п. а) достаточно иметь всего 5, а в п. б) - 6 сопротивлений.

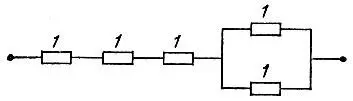
Рис. 6

а) Соединив параллельно два единичных сопротивления, получим сопротивление 1/ 2. Присоединив к нему последовательно еще три единичных сопротивления, мы получим сопротивление 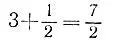(рис. 6).

б) С учетом разложения 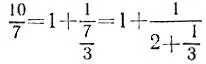требуемое сопротивление можно получить следующим образом: соединим последовательно одно единичное сопротивление и блок, в котором параллельно соединены три сопротивления - два единичных и блок из трех последовательных единичных сопротивлений (рис. 7). Тогда сопротивление второго блока будет равно 3, а первого - будет равно 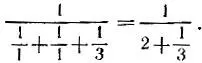Общее же сопротивление как раз и будет составлять 10/ 7.

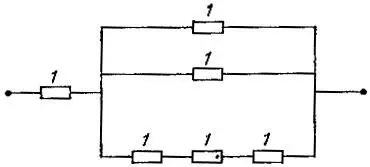
Рис. 7

в) Пусть дробь a/ bразложена в цепную дробь (см. задачу 5.7)

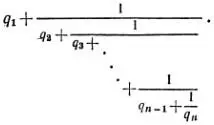
Тогда соединим последовательно q 1единичных сопротивлений и первый блок, в котором соединим параллельно q 2единичных сопротивлений и второй блок, в котором соединим последовательно q 3единичных сопротивлений и третий блок и т. д. Так, чередуя последовательное и параллельное соединения при составлении каждого последующего блока, мы на предпоследнем шаге соединим последовательно или параллельно q n-1единичных сопротивлений и (n-1)-й блок, в котором соединим, наоборот, параллельно или последовательно q nединичных сопротивлений. Всего нам понадобится q 1+ q 2+ ... + q n сопротивлений, что, как правило, меньше, чем a*b.

Докажем, что полученная схема имеет сопротивление a/ b. Если мы временно отсоединим от цепи весь первый блок, то сопротивление будет равно q 1, т. е. первой подходящей дроби к данной цепной дроби. Если временно отсоединим от цепи не первый, а второй блок, то сопротивление неполного первого блока будет равно 1/ q 2и общее сопротивление будет равно 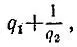т. е. второй подходящей дроби. Если отсоединим от цепи не второй, а третий блок, то сопротивление неполного второго блока будет равно q 3, первого -

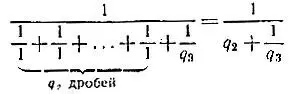
и общее сопротивление будет равно третьей подходящей дроби. Продолжая эти рассуждения до конца, мы придем к тому, что если отсоединить только (n-1)-й блок, то общее сопротивление будет равно (n-1)-й подходящей дроби. Наконец, если ничего не отсоединять, то общее сопротивление будет равно последней подходящей дроби, т. е. самой цепной дроби, равной a/ b.

5.12.а) Так как 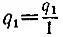- несократимая дробь, то P 1= q 1, Q 1= 1. Так как 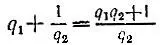- несократимая дробь, то P 2= q 1q 2+ 1, Q 2= q 2. Для k = 3 получаем

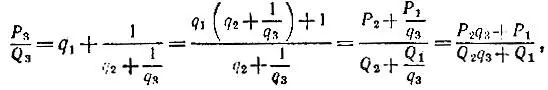
откуда имеем Р 3= Р 2q 3+ Р 1, Q 3= Q 2q 3+ Q 1, т. е. при k = 3 формулы справедливы, Пусть они уже доказаны для значения k-1:

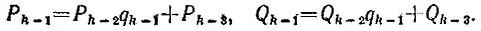
Тогда, заменяя q k-1выражением 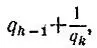мы из дроби 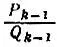получим k-ю подходящую дробь

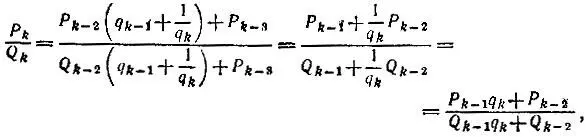
откуда имеем P k= Р k-1q k+ Р k-2, Q k= Q k-1q k+ Q k-2, т.е. формулы справедливы и для значения k (несократимость каждой из дробей 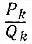была доказана в решении задачи 5.9).

б) В силу формул п. а) при k = 2, ..., n имеем

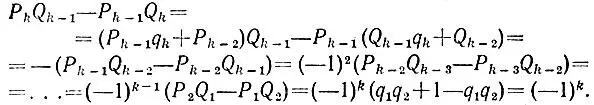
Поэтому для любого значения k = 2, ..., n получаем

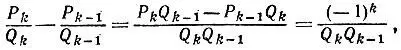
что и требовалось доказать,

5.13.Если бы мы захотели приблизить данную дробь 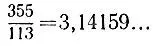десятичной дробью 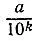то для достижения заданной точности потребовалось бы подобрать значения a и k из неравенства 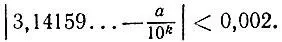Проверка дробей 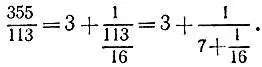показывает их непригодность и убеждает нас в том, что такой перебор значений весьма затруднителен, да и вряд ли приведет к успеху".

Попробуем приблизить данную дробь с помощью подходящих дробей к цепной дроби

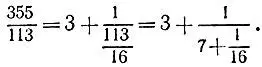
Первая подходящая дробь 3/ 1 дает погрешность 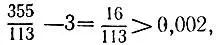а значит, не годится. Зато вторая подходящая дробь, равная 22/ 7 , отличается от третьей, равной исходной дроби, на величину