Сергей Гашков - Примени математику

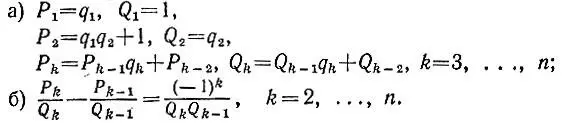
5.13. Приближение цепной дробиМежду двумя параллельными осями вращения требуется так установить зубчатую передачу, чтобы отношение угловых скоростей вращения было по возможности более близким к числу 355/ 113. Один из способов состоит в том, чтобы получить точное значение указанного отношения, поместив на одной оси шестеренку с 355 зубьями, а на другой - со 113 зубьями. Нельзя ли подобрать две шестеренки имеющие меньше 25 зубьев каждая, обеспечив при этом абсолютную погрешность, не превышающую 0,002?

5.1.а) Так как 36 = 2 2*3 2и 20 = 2 2*5, то (36, 20) = 2 2= 4.

б) Так как 1365 = 3*5*7*13 и 1225 = 5 2*7 2, то (1365, 1225) = 5*7 = 35.

в) Так как 1189 = 29*41 и 589 = 19*31, то (1189, 589) = 1.

5.2.Докажем, что все общие делители пары чисел а и b являются общими делителями пары чисел b и r и, наоборот, все общие делители пары чисел b и r являются общими делителями пары чисел а и b. Тогда и наибольшие общие делители обеих пар будут совпадать.

Пусть d - какой-нибудь общий делитель чисел а и b. Так как a = qb + r , то число r = a - qb также делится на d (ибо оно есть разность чисел а и qb, кратных d). Поэтому число d является общим делителем чисел b и г. Аналогично, если числа b и r имеют общий делитель d, то тот же делитель будет иметь и число a = qb + r , т. е. число d будет общим делителем чисел а и b.

В случае r = 0 получаем, что наибольший общий делитель пары чисел а и b равен наибольшему делителю числа b (не равного нулю), т. е. самому числу b.

5.3.Заметим, что остаток от деления любого числа на число а обязательно меньше самого числа а. Поэтому последовательность ненулевых остатков удовлетворяет неравенствам

a 2>a 3>a 4>a 5>...>0 и не может быть бесконечной, так как она содержит не более a 2чисел. Следовательно, описанный алгоритм не может продолжаться бесконечно. Если же число a nразделится на а n+1нацело, то, согласно результату задачи 5.2, будут выполнены равенства

(a 1, a 2) = (a 2, a 3) = (a 3, a 4) = ... = (a n, a n+1) = a n+1,т. е. наибольший общий делитель пары чисел a 1и a 2будет равен a n+1.

5.4.а) Так как

36 = 1*20 + 16, 20 = 1*16 + 4, 16 = 4*4,

то (36, 20) = 4.

б) Так как

1365 = 1*1225 + 140, 1225 = 8*140 + 105, 140 = 1*105 + 35, 105 = 3*35,

то (1365, 1225) = 35.

в) Так как

1189 = 2*589 + 11, 589 = 53*11 + 6, 11 = 1*6 + 5, 6 = 1*5 + 1, 5 = 1*5,

то (1189, 589) = 1.

5.5.Найдем наибольший общий делитель пары чисел, стоящих в числителе и знаменателе дроби, и сократим дробь на этот делитель.

а) Воспользуемся алгоритмом Евклида:

2147 = 1*1577 + 570, 437 = 3*133 + 38,

1577 = 2*570 + 437, 133 = 3*38+19,

570 = 1*437 + 133, 38 = 2*19,

откуда (2147, 1577) = 19. Произведя деление числителя и знаменателя дроби на 19, находим

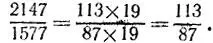
б) Заметим вначале, что числитель и знаменатель исходной дроби делятся на 6, поэтому ее можно сократить на 6 и получить дробь 221/ 2023. Теперь применим алгоритм Евклида:

2023 = 9*221 + 34, 221 = 6*34 + 17, 34 = 2*17.

Таким образом, (2023, 221) = 17 и дробь можно сократить еще на 17:

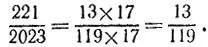
5.6.Из прямоугольника размером 135*40 сначала вырезаны квадраты со стороной, равной меньшей стороне этого прямоугольника, т.е. 40. Количество таких квадратов равно частному от деления 135 на 40 с остатком:

135 = 3*40 + 15.Из оставшегося прямоугольника размером 40*15 вырезаны квадраты со стороной 15, которых, согласно делению 40 на 15 с остатком

40= 2*15 + 10,можно вырезать два. Из оставшегося прямоугольника размером 15*10 вырезан один квадрат со стороной 10, что соответствует делению 15 на 10 с остатком:

15 = 1*10 + 5.Наконец, последний прямоугольник размером 10*5 разрезан на два квадрата со стороной 5, так как

10 = 2*5.Как показывает приведенный анализ, рассмотренный способ разрезания на квадраты прямоугольника размером а 1*а 2 , по существу, является демонстрацией алгоритма Евклида нахождения наибольшего общего делителя пары чисел а 1= 135 и а 2= 40 . Вообще прямоугольник размером а 1*а 2 можно разрезать на квадраты со сторонами а 2, а 3, а 4, ..., а n+1в полном согласии с формулами алгоритма Евклида (см. задачу 5.3), причем последовательные частные q 1, q 2, ..., q n укажут количества соответствующих квадратов.

5.7.Цепочку равенств, получающихся при нахождении наибольшего общего делителя пары чисел а 1и а 2с помощью алгоритма Евклида (см. задачу 5.3), перепишем следующим образом:

Подставляя в первую строчку вместо дроби а 2/ а 3ее выражение из второй строчки, находим

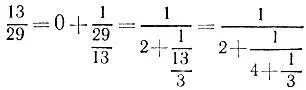
Подставляя сюда вместо дроби а 3/ а 4ее выражение из третьей строчки, имеем

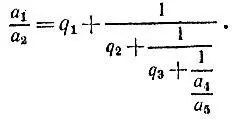
Производя аналогичные подстановки и далее, из предпоследней строчки получим равенство

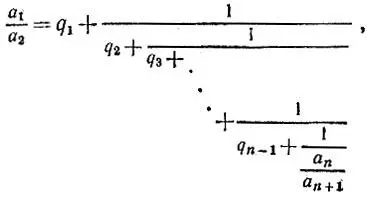
в котором останется лишь подставить вместо дроби 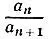ее значение q nиз последней строчки, после чего выражение будет удовлетворять всем требованиям задачи: все числа q 2, q 3, ..., q n являются натуральными, так как а 2>а 3>...>a n-1>a n>a n+1, а число q 1является целым (если a 1≥a 2, то натуральным, а если а 1<���а 2, то нулевым).

5.8.

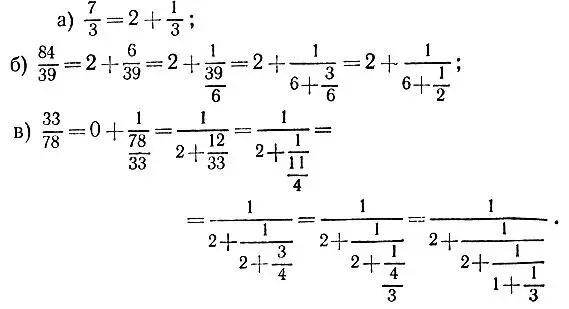
5.9.Последовательные операции по свертыванию цепной дроби сводятся к операциям двух типов: сложение 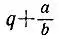и деление 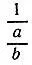. Докажем, что если a/ bнесократимая дробь, то в результате операции любого из указанных двух типов получается также несократимая дробь. Действительно, операция первого типа приводит к дроби 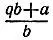, числитель и знаменатель которой не имеют общих делителей, поскольку (см. решение задачи 5.2) справедливы равенства (qb + a, b) = (b, a) = 1. Операция второго типа приводит к дроби b/ aкоторая также несократима, ибо (a, b) = (b, а) = 1. Таким образом, раз дробь 1/ q nнесократима, то на каждом шагу, в том числе и на последнем, при свертывании цепной дроби мы получаем несократимую дробь.