Сергей Гашков - Примени математику
- Название:Примени математику
- Автор:
- Жанр:
- Издательство:Наука
- Год:1989
- Город:Москва
- ISBN:5-02-013946-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Сергей Гашков - Примени математику краткое содержание
Рассматриваются вопросы построения и изменения ограниченными средствами, поиска оптимального решения в той или иной ситуации, способы быстрого счета, задачи на разрезание, переливание, взвешивание и т. п.
Для школьников и всех любителей математики.
Источник:
Примени математику - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
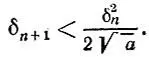
Каждое из чисел
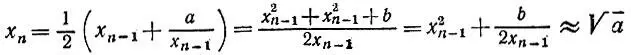
фактически получается с помощью приближенной формулы корня квадратною (см. задачу 3.11) из числа а по грубому приближению х n-1и остатку b. Поэтому предложенный способ представляет собой не что иное, как многократное применение этой формулы.
Для нахождения 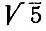 возьмем х 0= 2 и получим, согласно алгоритму,
возьмем х 0= 2 и получим, согласно алгоритму,
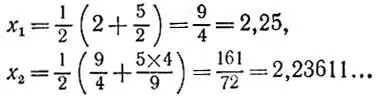
Оценим погрешность приближения:
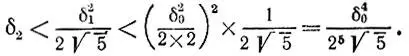
Так как  то
то

а значит, приближение 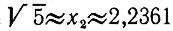 сразу гарантирует три верных знака после запятой (а на самом деле даже четыре знака),
сразу гарантирует три верных знака после запятой (а на самом деле даже четыре знака),
3.13.Пусть число х составлено из n первых цифр ответа, а число b равно указанной в условии разности (полученной на последнем шаге алгоритма задачи 3.9). Тогда без ограничения общности можно считать, что число х целое (см. задачу 3.3) и x≥10 n-1, а искомый корень равен х + 8 и δ<1. Погрешность приближения
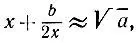
согласно утверждениям задачи 3.12, не превосходит числа
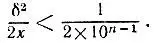
Таким образом, приближенное значение превышает точное, но менее чем на половину единицы (n-1)-го разряда после запятой, т. е. оно, по существу, задает еще n-1 верных знаков корня 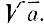
Применяя доказанный факт к полученным в решении задачи 3.10 значениям х = 223 606 и b = 356 764, находим частное 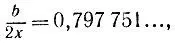 дающее следующие пять верных цифр корня:
дающее следующие пять верных цифр корня:

3.14.Возводя в куб обе части равенства

получаем
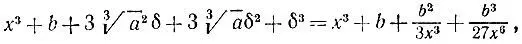
откуда имеем

Если х - наибольшее натуральное число, куб которого не превосходит искомого корня кубического, то справедливы неравенства
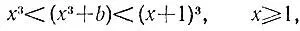
из которых получаем оценки
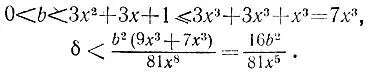
Наконец, для  приближенная формула дает значение
приближенная формула дает значение

с точностью до 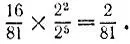
§ 4. Простое или составное?

При решении многих практических задач, в которых участвуют натуральные числа, немаловажную роль играет разложение этих чисел на множители, Основными "кирпичиками" в таком разложении являются простые числа, т. е. числа, большие 1 и делящиеся только на 1 и на себя. Остальные натуральные числа, большие 1, называются составными (число 1 не относится ни к простым, ни к составным). Основная теорема арифметики гласит, что всякое натуральное число, кроме 1, может быть представлено в виде произведения простых множителей, причем это представление единственно, если отвлечься от порядка множителей.
Издавна математиков интересовали вопросы о количестве и других свойствах простых чисел, а также о возможностях разложения конкретных чисел на простые множители. Еще Евклидом было доказано, что простых чисел бесконечно много. Древнегреческому математику Эратосфену был известен удобный способ отыскания простых чисел, который был назван решетом Эратосфена. Благодаря титаническим усилиям ряда ученых удалось получить ответы на многие, но пока не на все вопросы, связанные с распределением простых чисел в натуральном ряду. Что же касается разложения чисел на простые множители, то эта задача для больших чисел остается довольно трудной и по сей день.
4.1. Составные числаДокажите, что составных чисел бесконечно много,
4.2. Теорема ЕвклидаДокажите, что простых чисел бесконечно много.
4.3. Простые числа - соседиМогут ли два простых числа оказаться идущими подряд? А три?
4.4. Составные числа - соседиНайдите пять последовательных натуральных чисел, каждое из которых является составным. Для любого ли натурального значения n можно подобрать n таких чисел?
4.5. Простое или составное?Чтобы узнать, является ли данное натуральное число n составным, достаточно проверить, имеет ли оно хотя бы один делитель, больший 1 и меньший n. Докажите, что эту работу можно сократить, ограничившись проверкой делимости числа n только на простые числа и к тому же не превосходящие 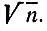
4.6. Простое или составное?Разложить на простые множители число: а) 315; б) 127; в) 1001; г) 899; д) 919.
4.7. Решето ЭратосфенаВыпишем подряд все натуральные числа от 1 до некоторого числа п и зачеркнем число 1. Возьмем первое незачеркнутое число, большее 1,- это будет число 2,- и зачеркнем каждое второе число, начиная отсчет от числа 2+1. Затем возьмем первое незачеркнутое число, большее 2,- это будет число 3,- и зачеркнем каждое третье число, начиная отсчет от числа 3 + 1 (ранее зачеркнутые числа также отсчитываются). Затем возьмем первое незачеркнутое число, большее 3,- это будет число 5,- и зачеркнем каждое пятое число, начиная отсчет от числа 5 + 1 . Продолжая действовать так и далее, остановимся тогда, когда первое незачеркнутое число, большее предыдущего, окажется большим 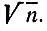 Докажите, что в итоге незачеркнутыми останутся все простые числа, не превосходящие n, и только они.
Докажите, что в итоге незачеркнутыми останутся все простые числа, не превосходящие n, и только они.
Интервал:
Закладка:










