Сергей Гашков - Примени математику

3.1.Пусть число а содержит в десятичной записи m знаков до запятой. Тогда справедливы оценки

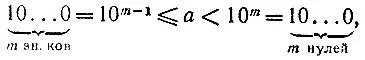
из которых следует, что квадрат числа а имеет либо 2m, либо 2m-1 знаков до запятой, так как

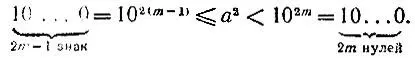
Поэтому если данное число имеет четное число n = 2m знаков или нечетное число n = 2m-1 знаков до запятой, то корень квадратный из него имеет m знаков до запятой.

Обычно, чтобы найти количество знаков корня квадратного, цифры десятичной записи исходного числа разбивают на группы справа налево, начиная от запятой и включая в каждую группу по две цифры (кроме, быть может, самой левой группы, в которой в случае нечетного количества этих цифр окажется только одна цифра). Тогда количество полученных групп как раз и совпадет с искомым количеством знаков корня.

3.2.Как и в решении задачи 3.1, заметим, что если число а содержит в десятичной записи m знаков до запятой, то его куб имеет либо 3m, либо 3m-1, либо 3m-2 знака до запятой, так как

Поэтому искомое количество знаков корня кубического совпадает с количеством групп, на которые разбиваются

цифры десятичной записи исходного числа справа налево, считая от запятой по три цифры в группе (кроме, возможно, последней группы).

Аналогично искомое количество знаков корня k-я степени равно количеству групп по k цифр (в последней группе может быть менее k цифр), на которые разбиваются цифры десятичной записи исходного числа, считая от запятой. Это вытекает из неравенств

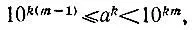
справедливых для любого числа а, имеющего в десятичной записи m знаков до запятой.

3.3.Для того чтобы свести извлечение корня k-й степени из конечной десятичной дроби к извлечению корня k-й степени из целого числа, достаточно в исходной дроби перенести запятую вправо на подходящее число qk разрядов, а затем извлечь корень из полученного целого числа и перенести запятую у результата влево на q разрядов. Справедливость этого утверждения основывается на равенстве

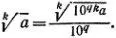
Из этого же равенства получаем зависимость между числами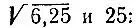

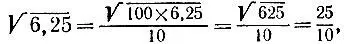
а для чисел зависимость далеко не так удобна:

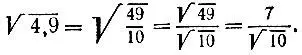
3.4.Так как 1728 = 2 6*3 8 , то нацело из числа 1728 извлекается только корень кубический

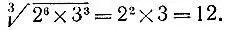
Дело в том, что показатели 6 и 3 степеней, в которых простые множители входят в разложение данного числа, имеют лишь один общий делитель, отличный от 1. Этот общий делитель - число 3 - как раз и указывает на возможность извлечения корня соответствующей (третьей) степени.

3.5.Возведем каждое из целых чисел от 0 до 9 в пятую степень:

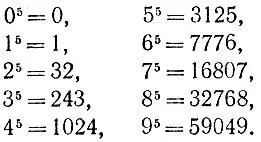
Заметим, что каждое из полученных в результате чисел оканчивается той же цифрой, что и соответствующее основание пятой степени. Тот же вывод можно распространить и на случай, когда основанием пятой степени является многозначное целое число, поскольку последняя цифра результата при этом полностью определяется последней цифрой основания степени.

Теперь при извлечении корня пятой степени из данного числа в предположении, что этот корень извлекается нацело, очень легко определяется последняя цифра корня - она просто совпадает с последней цифрой данного числа. Например, последняя цифра корня 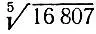равна 7, однако искомый корень имеет в десятичной записи всего одну цифру до запятой (см. задачу 3.2), а значит, этот корень просто равен 7, что подтверждается приведенными выше вычислениями.

Аналогично легко определяется последняя цифра 3 корня 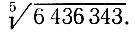Что же касается предпоследней цифры корня (а согласно решению задачи 3.2, если этот корень целый, то он представляет собой двузначное число), то ее можно определить с помощью сравнений:

20 5= 32'00000≤64'36343≤243'00000 = 30 5,из которых следует, что искомый корень удовлетворяет неравенствам

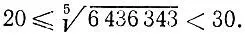
Поэтому первая его цифра не может быть никакой другой цифрой, кроме 2. Следовательно, сам корень равен 23, что подтверждается непосредственной проверкой возведением его в пятую степень.

3.6.Возведем каждое из целых чисел от 0 до 9 в куб:

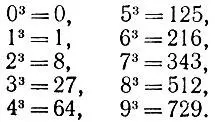
Заметим, что все полученные в результате числа оканчиваются разными цифрами. Проанализировав, какими именно цифрами они оканчиваются, заключаем, что последняя цифра куба любого целого числа либо совпадает с последней цифрой основания (если эта цифра есть 0, 1, 4, 5, 6 или 9), либо совпадает с дополнением последней цифры основания до 10 (если эта цифра есть 2, 3, 7 или 8).

Таким образом, последняя цифра числа 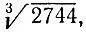если это число является целым, однозначно определяется последней цифрой его куба 2744, стало быть, она равна 4. Отбрасывая три последние цифры числа 2744, мы получаем число 2, которое расположено между кубами чисел 1 и 2, поэтому первая цифра искомого корня (а их всего две согласно решению задачи 3.2) равна 1:

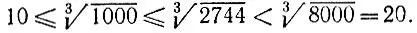
Итак, искомый корень равен 14, что подтверждается проверкой.

Наконец, аналогично находим, что последняя цифра числа 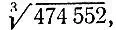если это число является целым, равна 8, а первая (она же предпоследняя) равна 7, так как 7 3= 343≤474≤8 3= 512 , т. е. это число равно 78, что затем проверяется непосредственно.