Сергей Гашков - Примени математику

2.24.Учитывая равенство 1001 = 7*11*13 , получаем, что недостаток m 1 при делении числа 103 (на любое из чисел 7, 11, 13) равен -1. Остаток m 2 от деления числа 10 3 равен остатку от деления числа 10 3m 1= -1000 = -1001 + 1 , т. е. равен 1. Недостаток m 3 от деления числа 10 6, равен недостатку от деления числа 10 3m 2= 1000 = 1001 - 1 , т.е. равен -1, и т. д. Поэтому если все цифры числа n разбиты на тройки, образующие трехзначные числа n 0, n 1, n 2, n 3, ..., n k (начиная справа), то число

n = n 0+10 3n 1+10 6n 2+10 9n 3+ ...+10 3kn k

дает при делении на любое из чисел 7, 11, 13 тот же остаток, что и число

n 0-n 1+n 2-n 3+. ..+(-1) kn k

Такие же рассуждения можно применить к указанной сумме еще и еще раз до тех пор, пока не получится трехзначное число (возможно, отрицательное). Остаток от деления этого числа на 7, 11, 13 будет таким же, как и у исходного числа n.

2.25.Заметим, что число 10m - 1 не имеет общих делителей с числом 10, так как око не делится ни на 2, ни на 5. Поэтому число n + n 0m делится на 10m - 1 тогда и только тогда, когда на 10m - 1 делится число

10 (n + n 0m) = 10n + 10mn 0= (10n + n 0)+ (10m - 1)n 0,т. е. когда на 10m - 1 делится первое выражение 10n + n 0 в полученном представлении. Полагая в доказанном утверждении m = 2 , получаем, что число 10n + n 0 делится на 19 только одновременно с числом n + 2n 0 . Таким образом, мы имеем следующий признак делимости на 19. В данном числе 10n + n 0 отбросим последнюю цифру n 0и, удвоив ее, прибавим к числу я, составленному из остальных цифр исходного числа. Проделав эту процедуру несколько раз, придем к не более чем двузначному числу, которое будет делиться на 19 в том и только в том случае, если на 19 делилось исходное число. Например, для числа 3 086 379 получаем последовательность чисел 308 655, 30 875, 3097, 323, 38, последнее из которых, а значит, и исходное кратно 19.

2.26.Так как число 10m + 1 взаимно просто с числом 10, то число n - n 0m делится на 10m + 1 только одновременно с числом

10 (n - n 0m) = 10n - 10mn 0= (10n + n 0) - (10m + 1)n 0,т. е. одновременно с числом 10n + n 0. Полагая в доказанном утверждении m = 3 , получаем следующий признак делимости на 31. В данном числе 10n + n 0 отбросим последнюю цифру n 0и, утроив ее, вычтем из числа n, составленного из остальных цифр исходного числа. Повторяя эту процедуру, мы придем к не более чем двузначному числу (возможно, отрицательному), которое будет делиться на 31 только одновременно с исходным числом. Например, для числа 2 886 379 имеем последовательность чисел 288 610, 28 861, 2883, 279, 0, последнее из которых, а значит, и исходное кратно 31.

2.27.Число 10m + 3 не имеет общих делителей с числом 10, так как оно не делится ни на 2, ни на 5. Поэтому число n + n 0(3m + 1) делится на 10m + 3 только одновременно с числом

10(n + n 0(3m + 1)) = (10n + n 0) + (30m + 9)n 0= (10n + n 0) + 3(10m + 3)n 0,т. е. одновременно с числом 10n + n 0. Полагая m = 1, получаем признак делимости на 13, согласно которому, отбросив в данном числе последнюю цифру n 0и прибавив учетверенную (3m + 1 = 4) эту цифру к числу n, составленному из остальных цифр исходного числа, получим число, которое будет делиться на 13 только одновременно с исходным числом. Учитывая признак делимости на 13, описанный в задаче 2.24, мы рассмотрим указанную схему лишь в применении к трехзначным числам. Например, для числа 481 последовательно получаем числа 52, 13, последнее из которых, а значит, и исходное кратно 13.

2.28.Так как число 10m - 3 взаимно просто с числом 10, то число n - n 0(3m - 1) делится на 10m - 3 только одновременно с числом

10 (n - n 0(3m - 1)) = (10n + n 0) - (30m - 9)n 0= (10n + n 0) - 3(10m - 3)n 0,т. е. одновременно с числом 10n + n 0. Полагая m = 2 , получаем признак делимости на 17, согласно которому, отбросив в данном числе последнюю цифру n 0и вычтя упятеренную (3m - 1 = 5) эту цифру из числа n, составленного из остальных цифр исходного числа, мы получим число, которое будет делиться на 17 только одновременно с исходным числом. Например, применяя эту процедуру несколько раз к числу 1067 481, последовательно получим числа 106 743, 10 659, 1020, 102,0, последнее из которых, а значит, и исходное, делится на 17.

Одной из наиболее трудоемких арифметических операций является извлечение корня квадратного, кубического или другой степени из данного числа. Относительно просто корень можно найти в том случае, когда заранее известно, что он представляет собой целое число, т. е. извлекается нацело. В некоторых случаях при извлечении корня приходится искать лишь приближенное его значение с наперед заданной точностью. Напомним, что приближенным значением величины а с точностью до числа σ>0 называется любое (вообще говоря, не единственное) число х, удовлетворяющее оценкам

а - δ≤x≤a + δ.Приближенное равенство π≈3,14, к примеру, означает, что число 3,14 есть приближенное значение числа n с точностью до половины единицы последнего разряда, т. е. до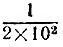

В настоящем параграфе вы познакомитесь с некоторыми методами нахождения корней, позволяющими довольно скоро и без особых усилий получать вполне удовлетворительные приближения.

3.1. Сколько знаков до запятой?Десятичная запись данного числа имеет n знаков до запятой. Можно ли заранее сказать, сколько знаков до запятой будет иметь десятичная запись корня квадратного из данного числа?

3.2. Корни других степенейКак по количеству знаков до запятой в десятичной записи данного числа определить количество знаков до запятой в десятичной записи корня кубического или корня другой степени из этого числа?

3.3. Сведение к целому числуКаким образом можно свести извлечение корня какой-либо степени из конечной десятичной дроби к извлечению корня той же степени из целого числа? Как связаны между собой числа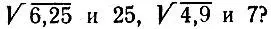

3.4. Разложив на простые множителиРазложив целое число на простые множители, можно определить, извлекается ли из него нацело корень данной степени. Попробуйте таким путем определить, корни каких степеней извлекаются нацело из числа 1728.

3.5. Корень пятой степени в умеВозведите в пятую степень каждое из чисел 0, 1, 2, ..., 9 и придумайте способ быстрого извлечения корня пятой степени из данного целого числа, имеющего в десятичной записи не более 10 знаков, в предположении, что этот корень извлекается из данного числа нацело.

Найдите корни