Сергей Гашков - Примени математику

Пользуясь тем, что число 10 3дает при делении на 37 остаток 1, получите следующий признак делимости на 37: если разбить все цифры числа n на тройки, начиная справа (в последней "тройке" может оказаться менее трех цифр, но тогда ее недостающие цифры будем считать нулями), и сложить эти тройки как трехзначные числа, то полученная сумма будет иметь тот же остаток от деления на 37, что и число n.

Придумайте способ, как упростить проверку делимости трехзначного числа на 37.

2.24. Общий признак для 7, 11, 13Пользуясь описанной в задаче 2.23 идеей разбиения цифр на группы, предложите признаки делимости на 7, 11, 13, сводящиеся к проверке делимости некоторого трехзначного числа на 7, 11, 13 соответственно.

2.25. Делимость на 19Докажите, что число 10n + n 0 делится на 10m - 1 только одновременно с числом n + n 0m . С помощью этого утверждения получите признак делимости на 19.

2.26. Делимость на 31Докажите, что число 10n + n 0 делится на 10m + 1 только одновременно с числом n - n 0m . С помощью этого утверждения получите признак делимости на 31.

2.27. Еще о делимости на 13Докажите, что число 10n + n 0 делится на 10m + 3 только одновременно с числом n + n 0(3m + 1). с помощью этого утверждения получите признак делимости на 13.

2.28. Делимость на 17Докажите, что число 10n + n 0 делится на 10m - 3 только одновременно с числом n - n 0(3m - 1) . С помощью этого утверждения получите признак делимости на 17.

2.1.Число делится на 5 в том и только в том случае, если его последняя цифра равна 0 или 5. Действительно, если последняя цифра числа n равна n 0, то само число n имеет вид 10n 1+ n 0. Так как число 10n 1 делится на 5, то остаток от деления числа n на 5 совпадает с остатком от деления на 5 цифры n 0. Поэтому остаток от деления числа на 5 равен нулю в том и только в том случае, если его последняя цифра делится на 5, т. е. равна 0 или 5.

2.2.Запишем данное число n в виде 100n 1+ n 0, где n 0- двузначное число, образованное двумя последними цифрами числа n. Так как число 100n 1 делится на 25, то остаток от деления числа n на 25 равен остатку от деления на 25 числа n 0. Следовательно, число n делится на 25 в том и только в том случае, если остаток от деления числа n 0на 25 равен 0, т. е. если две последние цифры числа n образуют одну из четырех комбинаций 00, 25, 50 или 75.

2.3.Число n делится на 5 kв том и только в том случае, если на 5 kделится число n 0, полученное из числа n отбрасыванием всех его цифр, кроме k последних. Действительно, запишем число n в виде 10 kn 1+ n 0. Тогда число 10 kn 1 делится на 5 k, а значит, остатки от деления чисел n и n 0на 5 kсовпадают и, стало быть, могут равняться 0 только временно.

2.4.Число n делится на 2 kв том и только в том случае, если на 2 kделится число n 0, полученное из числа n отбрасыванием всех его цифр, кроме к последних. Данное утверждение следует из представления числа n в виде 10 kn 1+ n 0 и того факта, что число 10 kn 1делится на 2 k.

2.5.Проще всего в данном двузначном числе выделить наибольшее возможное четное число десятков (ведь любое число, кратное 20, кратно и 4), в результате чего останется число, меньшее 20, для которого проверка делимости на 4 уже не представляет труда. Например, число 76 = 60 + 16 делится на 4, а число 94 = 80 + 14 не делится.

2.6.Заметим, что любое четное число сотен делится на 8, а нечетное дает при делении на 8 остаток 4 и недостаток - 4. Поэтому, отбросив цифру сотен данного трехзначного числа, достаточно проверить, делится ли на 8 оставшееся двузначное число в чистом виде, если цифра сотен была четной, либо предварительно увеличенное или уменьшенное на 4, если цифра сотен была нечетной. Кроме того, для упрощения проверки делимости на 8 двузначного числа можно выделить в нем наибольшее возможное число десятков, кратное 4, в результате чего останется число, меньшее 40, для которого проверка делимости на 8 уже не представляет труда. Например, число 692 не делится на 8, так как 92 = 80 + 12 не делится на 8, а число 568 делится на 8, так как 68 - 4 = 64 делится на 8.

2.7.Пусть данное число n имеет вид

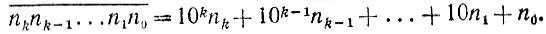
Поскольку 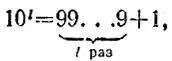то получаем

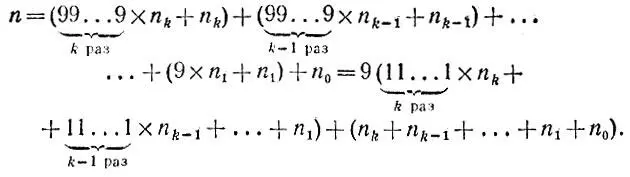
В полученном представлении числа n первое выражение делится как на 3, так и на 9, поэтому остатки от деления числа n и суммы всех его цифр n k+ n k-1+ ... + n 1+ n 0 как на 3, так и на 9 совпадают.

2.8.Для упрощения проверки делимости суммы цифр данного числа на 3 можно заменять цифры их остатками или недостатками от деления на 3. Например, сумма цифр числа 2 795 438 дает тот же остаток при делении на 3, что и сумма 2 + 1 + 0 - 1 + 1 + 0 - 1 = 2.

2.9.Для упрощения проверки делимости суммы цифр данного числа на 9 можно отбрасывать те цифры, которые в сумме дают 9 или 18. Например, сумма цифр числа 7 543 782 861 дает тот же остаток при делении на 9, что и число 6, поскольку сумма всех остальных цифр (7 + 2) + (5 + 4) + (3 + 7 + 8) + (8 + 1) кратна 9.

2.10.Пусть число m k-значное. Тогда среди чисел от 10 k+1 до 10 k+1+ m хотя бы одно число делится на m. Это число имеет вид 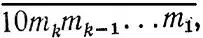, а так как признак делимости на m не зависит от порядка цифр делимого, то числа 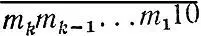и 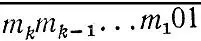также кратны m. Поэтому число m является делителем разности этих чисел, равной 9, а значит, либо m = 3, либо m = 9 (случай m = 1 исключен в условии задачи).

2.11.Описанная в задаче проверка сложения основана на том, что если при подсчете суммы нескольких чисел не было сделано ошибки, то эта сумма должна давать тот же остаток при делении на какое-либо число m, что и сумма остатков от деления слагаемых на m. При этом нахождение остатков от деления на m = 9 по сумме цифр не требует серьезных усилий, что и нашло отражение в предложенном способе. Если складывались числа разного знака, то сумма всех положительных слагаемых должна давать тот же остаток при делении на m, что и сумма всех отрицательных слагаемых вместе с полученным в ответе числом. Для нахождения этих остатков при m = 9 достаточно заменить сами числа суммами их цифр.