Сергей Гашков - Примени математику

1.16.Пусть нужно перемножить числа 10а+b и 10а+с , удовлетворяющие условию b+с = 10. Тогда имеем

b>(10а+b)(10а+с) = 100а 2+ 10aс + 10bа + bс = 100а 2+ 10а(b+с) + bс = 100а 2+ 100а + bс = 100а(а+1) + bc, что и требовалось доказать.

1.17.Для возведения в квадрат числа, оканчивающегося на 5, достаточно отбросить у него последнюю цифру, а затем перемножить полученное число с числом, большим его на 1, и приписать к результату справа 25. Это правило является следствием равенства, доказанного в решении задачи 1.16, если в нем положить b = с = 5.

1.18.Пусть перемножаются числа 10а+5 и 106+5. Правильность предложенного способа вытекает из следующих равенств:

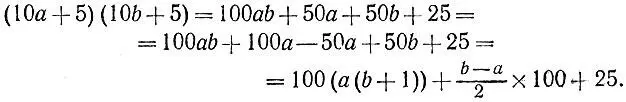
1.19.Произведение чисел а и b можно найти по формуле

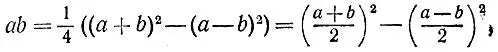
удобной для применения в случае одновременной четности или одновременной нечетности сомножителей (в противном случае их полусумма и полуразность были бы нецелыми) и в случае, когда эти сомножители близки друг к другу.

1.20.Квадраты двух соседних чисел различаются на сумму этих чисел, поскольку имеют место равенства

(а+1) 2- а 2= 2а + 1 = (а+1) + а.Аналогично, если числа различаются на 2, то разность их квадратов

(a+2) 2- а 2= 4а + 4 = 4(а+1) = 2((а+2) + а)равна удвоенной сумме этих чисел. Так как любое целое число отличается от ближайшего числа, кратного 5, не более чем на 2, то, пользуясь указанными здесь соображениями, можно восстановить его квадрат, например,

31 2= 30 2+ (31 +30) = 900 + 61 = 961, 32 2= 30 2+ 2 (32 + 30) = 900 + 124 = 1024, 33 2= 35 2- 2 (33+ 35) = 1225 - 136 = 1089, 34 2= 35 2- (34 + 35) = 1225 - 69 = 1156. 1.21.Кубы двух соседних чисел а и а+1 различаются на число

(а+1) 3- а 3= 3а 2+ 3а + 1 = 3а(а+1) + 1,равное утроенному произведению этих чисел, увеличенному на 1. Поэтому, зная куб, скажем, числа 30, мы быстро находим куб следующего числа:

31 3= 30 3+ 3*30*31 + 1 = 27 000 + 2790 + 1 = 29 791. 1.22.Вычисление квадратов в разобранных примерах основано на формуле

a 2= (а+b)(а-b) + b 2,в которой удачный подбор числа b сильно облегчает выкладки: во-первых, один из сомножителей должен оказаться "круглым" числом (желательно, чтобы ненулевой его цифрой была только первая), во-вторых, само число b должно легко возводиться в квадрат, т. е. должно быть небольшим. Эти условия реализуются как раз на числах а, близких к "круглым".

1.23.Пусть надо найти квадрат числа а, заключенного между 25 и 50. Тогда, пользуясь формулой из решения задачи 1.22, получаем

а 2- (а + (50-а)) (а - (50-а))+ (50-а) 2= 50 (2а-50) + (50-а) 2- (а-25)100 + (50-а) 2,откуда следует справедливость предложенного способа.

1.24.Приведенные в решении задачи 1.23 выкладки справедливы для любого числа а, поскольку они не используют оценок 25<���а<50. Для описания же процедуры возведения в квадрат двузначного числа а, большего 50, имеет смысл в соответствующем описании из условия задачи 1.23 "дополнение" числа а до 50 заменить дополнением 50 до числа а, а вычитание 25 из числа а - прибавлением 25 к уже найденному дополнению а - 50. Действительно, с учетом формулы из решения задачи 1.23 имеем

а 2= (а-25)100 + (50-а) 2- ((а-50)+25)100 + (а-50) 2.Например, при а = 63 получаем

63 2= (13 + 25)100 + 132 = 3969. 1.25.Для возведения в квадрат числа, близкого к 500, достаточно отнять от него 250 и, увеличив результат в 1000 раз, прибавить к нему квадрат разности между исходным числом и 500. Действительно, по аналогии с решением задачи 1.23 имеем

а 2- (а+ (500-а)) (а-(500-а)) + (500-а) 2= 500 (2а-500) + (500-а) 2= (а-250)1000 + (500-а) 2,а при а = 492 получаем разобранный в условии пример.

Вопрос о том, делится ли данное число n нацело на другое число m, часто возникает в самых разных практических задачах. Один из способов выяснить это состоит в непосредственном делении числа n на число m, однако такой способ далеко не самый легкий. Желание иметь какие-либо критерии, позволяющие устанавливать факт делимости, не прибегая к операции деления, приводит нас к задаче о нахождении наиболее простых признаков делимости.

Некоторые признаки делимости (на 2, на 3, на 5, на 9) хорошо известны. Целью настоящего параграфа является создание более или менее целостной картины, выработка единого взгляда на систему методов, дающих различные признаки делимости. Разумеется, свойства чисел настолько богаты и разнообразны, что их вряд ли можно уложить в одну простую схему, дающую все признаки делимости. Мы постарались отобрать лишь такие свойства, из которых получаются наиболее эффективные, на наш взгляд, результаты.

Для решения приведенных ниже задач могут понадобиться некоторые сведения о целых числах. Напомним, что деление числа n на число m с остатком означает нахождение частного q и остатка r, для которых выполнены условия

n = qm + r, 0≤rЕсли r = 0, то говорят, что число n делится на m или кратно m. Мы будем разрешать деление не только положительных чисел, но и любых целых чисел вообще - при этом число q, возможно, будет отрицательным или нулем. Будем допускать также и деление с недостатком -r, т. е. представление числа в виде

n = qm - r, 0≤rПолезно знать следующие несложные факты (если они вам не известны, то попробуйте доказать их самостоятельно):

а) если два числа отличаются друг от друга на число, кратное m, то остатки от деления этих чисел на m совпадают, и наоборот;

б) сумма двух чисел имеет тот же остаток от деления на m, что и сумма остатков от деления этих чисел на m;

в) произведение двух чисел имеет тот же остаток от деления на m, что и произведение остатков от деления этих чисел на m;

г) если произведение двух чисел, одно из которых взаимно просто с числом m, делится на m, то второе из этих чисел делится на m, и наоборот;

д) если число делится на каждое из двух взаимно простых чисел, то оно делится и на их произведение.

Число, десятичная запись которого состоит из k цифр n 1, n 2, ..., n k-1, n k , идущих справа налево, будем обозначать так: n kn k-1...n 2n 1 . При этом иногда под k-значным числом будем понимать также числа, имеющие на самом деле менее k цифр, не исключая возможности, что некоторые первые цифры числа являются нулями.

Решив предложенные в этом параграфе задачи, вы сможете конструировать свои, новые признаки делимости, а также научитесь использовать свойства делимости для контроля за правильностью арифметических действий.

2.1. Делимость на 5Сформулируйте и докажите признак делимости на 5. Как найти остаток от деления числа на 5?