Сергей Гашков - Примени математику

19.48.Например, годится следующая формула:

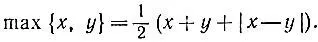
19.49.Достаточно сделать 5 поездок, так как за каждую поездку, кроме последней, можно увезти не менее 2 т . Меньше 5 поездок может не хватить, например, если весь груз расфасовать поровну в 13 ящиков.

19.50.Когда весы находятся в равновесии, отношение весов грузов, лежащих на чашках, есть фиксированная (обратная отношению плеч) величина а . Поэтому если отвесить по 1 кг сахара на каждой чашке весов, то на самом деле будет получено а + 1/ акг, что при а≠1 будет больше 2 кг. Чтобы отвесить ровно 2 кг сахара, достаточно весы с килограммовой гирей на одной чашке уравновесить любым грузом (например, тем же песком), а затем снять гирю и уравновесить весы сахаром. Мы получим ровно 1 кг сахара и аналогично еще 1 кг .

19.51.Если прикрепить гирю к одному концу линейки, а взвешиваемый груз к другому (рис. 156) и уравновесить

эту систему, правильно подобрав на линейке точку опоры, то отношение х:y расстояний по линейке от опоры до гири и до груза будет равно отношению весов груза и гири соответственно. Кстати, можно проградуировать линейку, написав возле нескольких возможных положений опоры заранее подсчитанные соответствующие веса груза.

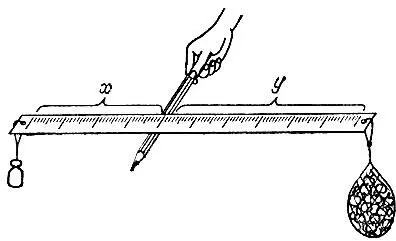
Рис. 156

19.52.Запомнив время на стенных часах, сходите и узнайте правильное время. Вернувшись домой, определите по стенным часам время вашего отсутствия и прибавьте половину этого времени к тому времени, которое вы видели на правильных часах. Это время и нужно установить на ваших часах.

19.53.Время t работы будет наименьшим, если обе машинистки закончат печатать одновременно, т. е. если первая машинистка напечатает t/ 6 листов, а вторая t/ 10 листов. Поэтому работу между ними нужно заранее распределить в пропорции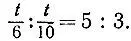

19.54.Если шины на передних колесах стираются за n км пути, а задние - за m км , то перестановка местами передних колес с задними после прохождения 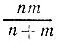км пути приводит к одновременному стиранию всех колес и максимально удлиняет пробег автомобиля без замены шин.

19.55.В результате внедрения всех трех изобретений производственные затраты могут составить минимум 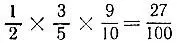прежних затрат. Поэтому они уменьшатся в лучшем случае на 73% (это если сами изобретения оказывают влияние на процесс производства не зависимым друг от друга образом).

19.56.Постоянно на лугу могут пастись максимум 15 коров. Если обозначить через х полное количество травы на лугу, а через y и z количества травы, вырастающей ежедневно на лугу и съедаемой одной коровой за один день соответственно, то будет справедлива система

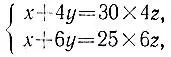
откуда 15z = y . Таким образом, трава на лугу растет с той же скоростью, с какой ее поедают 15 коров. Проверка показывает, что 16 коров съедят всю траву за 60 дней.

19.57.Парашютист мог обойти стену, все время держась за нее, скажем, левой рукой и замеряя углы поворотов, которые ему приходилось при этом делать. Подсчитав в конце алгебраическую сумму всех этих углов (со знаком плюс, если поворот был левым, и со знаком минус, если правым), он мог воспользоваться следующим фактом: сумма углов должна равняться либо -360°, если он находится внутри участка, либо 360°, если снаружи.

19.58.Если поворачивать табуретку в "плоскости" пола, то обязательно наступит такой момент, когда все 4 ножки табуретки будут касаться пола.

19.59.На рис. 157 показано, как, положив кирпич на угол стола, а затем передвинув его параллельно краю стола на длину соответствующего ребра кирпича, можно получить две точки (угол стола и вершина кирпича), расстояние между которыми как раз равно длине главной диагонали кирпича.

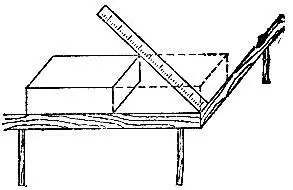
Рис. 157

19.60.Намотаем проволоку в один слой, например, на саму линейку так, чтобы соседние витки проволоки были плотно прижаты друг к другу (рис. 158). Тогда, поделив ширину полученного слоя на количество витков, мы получим толщину одного витка, которая совпадает с диаметром проволоки.

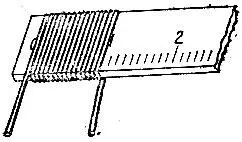
Рис. 158

19.61.Измерим внешний радиус R и внутренний радиус r рулона (рис. 159). Затем отмотаем такую часть ленты длиною l, чтобы при этом ощутимо уменьшился внешний радиус рулона. Если он уменьшился на d, то длина ленты приблизительно равна

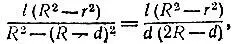
так как длина ленты в рулоне пропорциональна площади его поперечного сечения.

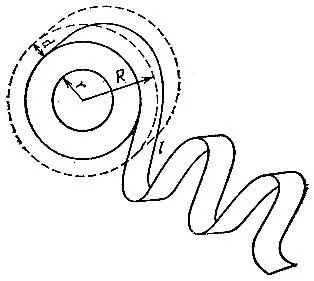
Рис. 159

19.62.Если на осколке сохранились хотя бы три точки края пластинки, то можно перенести их на бумагу и построить центр О окружности, проходящей через эти три точки (рис. 160). Радиус R этой окружности совпадает с радиусом пластинки. Впрочем, его можно и посчитать, измерив, скажем, попарные расстояния a, b и с между тремя указанными точками и воспользовавшись формулами

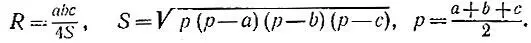
Рис. 160

19.63.Измерим длину l большой окружности шара, образовав из измерительной ленты наименьшее кольцо, через которое проходит шар. Тогда объем шара будет равен l 3/ (6π 2).

19.64.Если обозначить через H высоту маяка, а через R радиус Земли (R ≈ 6400 км) , то искомое расстояние будет равно (рис. 161)

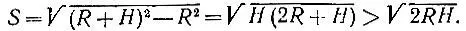
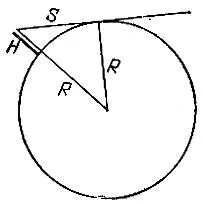
Рис. 161

При H = 125 м имеем S ≈ 40 км.

19.65.Возьмем две точки A и В на поверхности бильярдного шара и проведем на нем дуги равных радиусов с центрами в этих точках. В пересечении дуг получатся точки С и D, аналогично построим точку Е (рис. 162). Теперь, замерив циркулем длины отрезков CD, DE и СЕ, мы перенесем эти точки на бумагу с сохранением указанных длин и построим на бумаге центр О окружности, описанной вокруг получившегося треугольника. Радиус шара как раз и будет равен радиусу этой окружности.