Сергей Гашков - Примени математику

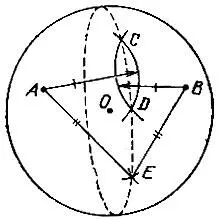
Рис. 162

19.66.Из всех прямоугольников фиксированного периметра наибольшую площадь имеет квадрат, так как величина площади прямоугольника размером а*(з - а) достигает наибольшего значения 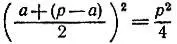при а = p - а .

19.67.Наибольшую площадь будет иметь палисадник, представляющий собой половину квадратного участка, т. е. имеющий две короткие стороны, равные половине длинной стороны, противолежащей стене дома.

19.68.Наибольший объем будет иметь коробка, высота h которой равна четверти стороны основания, поскольку учетверенный объем 4h(a - 2h) 2 коробки, сделанной из квадрата со стороной а , достигает наибольшего значения

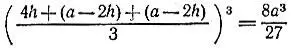
при 4h = a - 2h .

19.69.Если х, y и z - соответственно высота, ширина и длина коробка объемом V, то расход материала на его изготовление пропорционален величине 2xy + 3yz + 4xz , которая принимает наименьшее значение

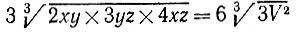
при 2xy = 3yz = 4xz, т. е. когда х:y:z = 3:4:2.

19.70.Кратчайший путь от лампочки А до выключателя В будет равен 40 м и пройдет он не только по потолку и торцевым стенкам (такой путь АВ 1на развертке, изображенной на рис. 163, имеет длину 42 м ), а также и по боковой стене (соответствующий путь на рис. 163 проходит по отрезку АВ 2).

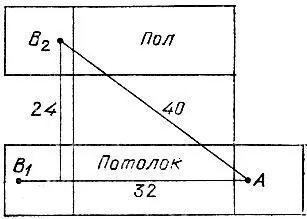
Рис. 163

19.71.Кратчайший путь от лампочки А до выключателя В имеет длину 5 м и показан на развертке бункера (рис. 164).

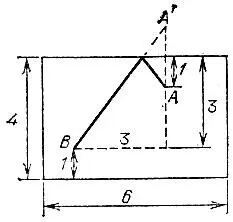
Рис. 164

19.72.Если разместить развертку пяти граней куба так, как изображено на рис. 165, то в четырех углах квадратной салфетки останутся четыре треугольника, которых будет достаточно для покрытия шестой грани куба (подсчет показывает, что нарисованный "крест" действительно помещается в квадрате и даже оставляет зазор шириной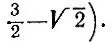

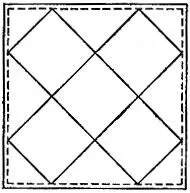
Рис. 165

19.73.Одна из вершин прямоугольника должна совпадать с серединой гипотенузы.

19.74.Через точку А, расположенную от вершины В угла вдвое дальше, чем данная точка С (рис. 166), проведем прямую, параллельную стороне угла. Она пересечет другую сторону угла в точке D, через которую и проходит искомая прямая.

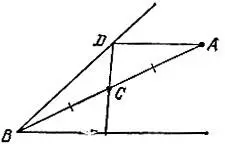
Рис. 166

19.75.Диаметром наименьшего круга, содержащего указанный треугольник, является наибольшая сторона этого тупоугольного треугольника, равная 4.

19.76.Крепче держится треугольный гвоздь, поскольку соприкасается с окружающей его древесиной по наибольшей поверхности: при равных площадях сечения периметр значения будет наибольшим у треугольника и наименьшим круга (отсюда, кстати, следует, что круглый гвоздь держится слабее любых других гвоздей).

19.77.Частей не могло быть 66, но могло быть 67, так при каждом измельчении листа число кусочков увеличивалось на 3, а вначале это число было равно 1.

19.78.На рис. 167 показано, как разрезать квадрат на 4, 6 или 8 квадратов. Деля любую из полученных частей на 4 квадрата, мы будем увеличивать их число на 3. Таким образом, из исходного квадрата можно получить разрезанием как 4 квадрата, так и любое их число, большее 5.

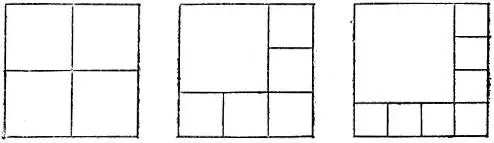
Рис. 167

19.79.Число разломов не зависит от порядка, в котором они производятся. Это число будет на единицу меньше, чем количество квадратных долек, составляющих плитку шоколада, поскольку после первого разлома образуются два куска шоколада, после второго-три, после третьего-четыре и т. д.

19.80.Достаточно двух цветов. Это доказывается индукцией по числу прямых линий, делящих страну на области.

19.81.Сложив лист пополам, разрежем его так, как показано на рис. 168.

Рис. 168

19.82.Разобьем имеющиеся треугольники на пары и сложим из них одинаковые параллелограммы, а затем замостим всю плоскость такими параллелограммами (рис. 169).

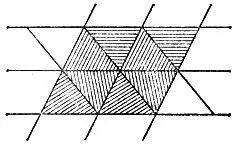
Рис. 169

19.83.Для паркета годятся любые одинаковые четырехугольники: сначала замостим всю плоскость параллелограммами, построенными на диагоналях данного четырехугольника как на сторонах, а затем в каждый параллелограмм поместим по данному четырехугольнику (на рис. 170 они заштрихованы), а остальные части плоскости автоматически окажутся такими же, но повернутыми четырехугольниками.

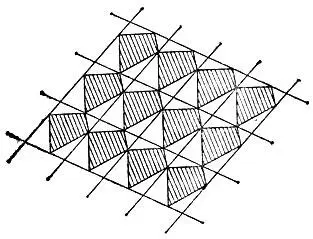
Рис. 170

19.84.Годится любая прямая, проходящая через точку пересечения диагоналей прямоугольника.

19.85.Достаточно провести разрез через центры симметрии прямоугольника и параллелограмма.

19.86.Достаточно, например, разрезать треугольник на три части, на которые его разбивают перпендикуляры к сторонам, опущенные из центра вписанной окружности (рис. 171).

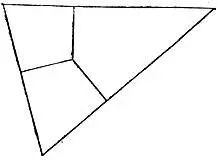
Рис. 171

19.87.Пусть требуется провести разрез через вершину А четырехугольника ABCD. Через середину О диагонали BD проведем прямую, параллельную другой диагонали АС, до пересечения со стороной ВС или CD в точке Е (рис. 172). Тогда прямая АЕ делит четырехугольник ABCD на равновеликие части.

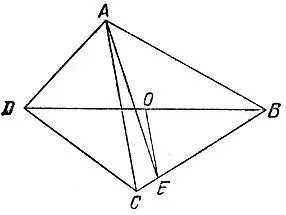
Рис. 172

19.88.Приставим один из меньших квадратов к другому и отрежем от них два исходных прямоугольных треугольника, переложив их так, как показано на рис. 173.

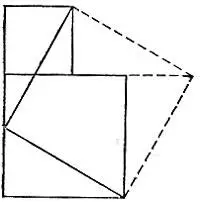
Рис. 173