Сергей Гашков - Примени математику

19.73. Наибольшая площадьИз прямоугольного треугольника нужно вырезать прямоугольник так, чтобы одна из его вершин совпадала с вершиной прямого угла треугольника, две другие вершины лежали на катетах и одна вершина на гипотенузе, а площадь его была наибольшей.

19.74. Наименьшая площадьЧерез данную точку внутри угла нужно провести прямую, отсекающую от угла треугольник наименьшей площади. Как это сделать?

19.75. Треугольник из кругаИз какого наименьшего бумажного круга можно вырезать треугольник, стороны которого равны 2, 3 и 4?

19.76. Лучший гвоздьВ бревно вбито три гвоздя одинаковой длины и массы, но разного сечения: круглый, квадратный и треугольный. Какой из гвоздей держится крепче?

19.77. Не пересчитывая ответЛист бумаги разорвали на 4 части, затем какие-то из этих частей разорвали на 4 части и т. д. Когда сосчитали общее число частей, то их оказалось то ли 66, то ли 67.

Можно ли, не пересчитывая, уточнить ответ?

19.78. На несколько квадратовБумажный квадрат требуется разрезать на несколько более мелких квадратов, не обязательно одинаковых. Каким может быть их количество?

19.79. Плитка шоколадаВы хотите разломать плитку шоколада на мелкие квадратные дольки, из которых она состоит. Какое наименьшее число разломов вам для этого потребуется сделать при условии, что разные куски шоколада нужно ломать отдельно?

19.80. Раскраска картыТерритория страны разбита на области прямыми линиями. Какое наименьшее число красок необходимо для такой раскраски карты страны, чтобы никакие две области, имеющие общую границу, не оказались одного цвета?

19.81. Огромная дыраСумеете ли вы разрезать лист из школьной тетради так, чтобы в итоге образовалось кольцо, через которое мог бы свободно пролезть взрослый человек?

19.82. Треугольный паркетИз правильных треугольников можно сложить паркет, т. е. замостить ими всю плоскость без наложений и дыр. А можно ли сложить паркет из произвольных неправильных, но все же одинаковых треугольников?

19.83. Четырехугольный паркетИз каких одинаковых четырехугольников можно сложить паркет?

19.84. Пятью прямымиПроведите 5 прямых, каждая из которых делит заданный прямоугольник на 2 равные части.

19.85. Дырявый прямоугольникВнутри прямоугольного листа бумаги вырезана дырка, имеющая форму параллелограмма (рис. 142). Предложите какой-нибудь способ, как разрезать этот лист на две части одинаковой площади.

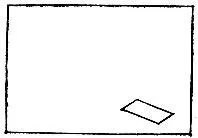
Рис. 142

19.86. Треугольник наизнанкуВы вырезали из цветной бумаги треугольник, да, как выяснилось, у него цветной оказалась не та сторона. Как разрезать этот треугольник на части, чтобы, перевернув их обратной стороной, можно было сложить его снова?

19.87. Площадь пополамИз бумаги вырезан выпуклый четырехугольник. По какой линии, проходящей через данную его вершину, нужно провести разрез, чтобы четырехугольник разделился на две части одинаковой площади?

19.88. Теорема ПифагораНа сторонах прямоугольного треугольника построены квадраты (рис. 143). Согласно теореме Пифагора, площадь наибольшего из них равна сумме площадей двух меньших.

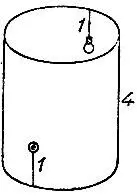
Рис. 143

Попробуйте продемонстрировать этот факт, вырезав два меньших квадрата и разрезав их на такие части, из которых можно составить большой квадрат.

19.89. Плотное заполнениеМожно ли ящик размером 20*15*14 заполнить коробками размером 3*5*10 так, чтобы в ящике не осталось пустот и из него не выступали коробки?

19.90. Заготовки для пельменейИз квадратного листа теста размером 8*8 нужно вырезать круги диаметром 1 для изготовления пельменей. Можно ли разместить на этом листе более 64 кругов?

19.91. На почтительном расстоянииМожно ли на круглом поле диаметром 1 км пробурить 125 скважин так, чтобы расстояние между любыми двумя скважинами было больше 100 м ?

19.92. Перпендикуляр к диаметруДана окружность диаметром АВ. Из некоторой точки, не лежащей на прямой АВ, нужно опустить перпендикуляр к этой прямой. Можно ли это сделать, используя только линейку (без делений)?

19.93. Вместо транспортира - линейкаС помощью линейки (без делений) с параллельными краями проведите биссектрису данного угла.

19.94. Угол с недоступной вершинойС помощью линейки с параллельными краями проведите биссектрису угла, вершина которого находится за пределами листа бумаги.

19.95. Разделить линейкой без деленийПри помощи линейки (без делений) с параллельными краями разделите отрезок пополам.

19.96. Центр окружностиПри помощи линейки с параллельными краями найдите центр данной окружности.

19.97. Двусторонней линейкойМожно ли с помощью двусторонней линейки построить перпендикуляр к данной прямой?

19.98. Линейкой с делениямиПри помощи обычной линейки с делениями проведите биссектрису данного угла.

19.99. Обыкновенным угольникомНайдите центр данной окружности при помощи угольника.

19.100. Найти серединуКак с помощью одного угольника разделить данный отрезок пополам?

19.101. Шоколадкой как линейкойВы положили плитку шоколада на бумагу, обвели ее карандашом и хотите найти точку пересечения диагоналей нарисованного прямоугольника. Можно ли это сделать, используя в качестве линейки ту же плитку, несмотря на то, что ее длины не хватает для проведения диагоналей?

19.102. К недоступному центруНа самом краю листа нарисована дуга окружности, центр которой не помещается на бумаге. Через данную точку проведите прямую, проходящую через этот центр.

19.103. Перпендикуляр на краю листаНа листе бумаги, имеющем рваный край (рис. 144), с помощью циркуля и линейки восстановите перпендикуляр

к прямой стороне АВ через ее концевую точку А.

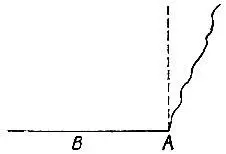
Рис. 144

19.104. Циркулем, но не окружностьМожно ли с помощью циркуля нарисовать на бумаге не окружность, а овал?

19.105. Точки на прямойС помощью одного лишь циркуля постройте несколько точек, лежащих на одной прямой с двумя данными точками.

19.106. Одним циркулемРазделите данный отрезок пополам, используя один лишь циркуль.

19.107. Заданные расстоянияС помощью одного циркуля по данным двум точкам, расстояние между которыми равно 1, постройте точки, на которых реализуются расстояния