Сергей Гашков - Примени математику

Если же у равностороннего пятиугольника ABCDE равны три диагонали, скажем AC, BD и СЕ (а на самом деле любые три диагонали - попробуйте доказать это самостоятельно), из равенства треугольников ABC, BCD и CDE (по трем сторонам) вытекает равенство углов пятиугольника при вершинах В, С и D (рис. 132). Кроме того, из равенства треугольников ABD и ACD (по трем сторонам) имеем ∠ BAD = ∠ CDA , откуда с учетом равнобедренности треугольника AED получаем равенство углов пятиугольника при вершинах А и D. Аналогично доказывается равенство углов при вершинах В и Е, т. е. равенство всех углов и, значит, правильность пятиугольника ABCDE.

Рис. 132

18.24.Условие а) в дополнение к тому, что три главные диагонали равностороннего шестиугольника пересекаются в одной точке, не обеспечивает его правильности. Например, вырожденный шестиугольник ABCDEF, превратившийся в прямоугольник и изображенный на рис. 133, удовлетворяет всем перечисленным условиям, но не является правильным.

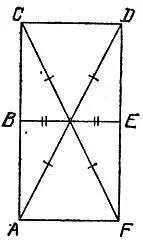
Рис. 133

Аналогично обстоит дело и с условием в), для которого контрпримером служит вырожденный шестиугольник ABCDEF, превратившийся в треугольник и изображенный на рис. 134 (в нем главные диагонали AD, CF и ЕВ равны и пересекаются в одной точке, неглавные диагонали образуют равносторонние треугольники АСЕ и BDF).

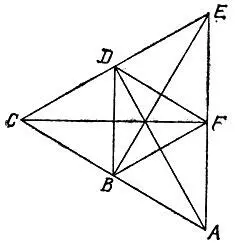
Рис. 134

Если же выполнено условие б), то около шестиугольника можно описать окружность с центром в точке пересечения его главных диагоналей, а коль скоро сам шестиугольник является еще и равносторонним, то он обязательно правильный (см. задачу 18.21).

18.25.Наименьшее число диагоналей, которое нужно проверить, равно четырем. В том, что трех диагоналей недостаточно, можно убедиться непосредственным перебором различных случаев. Если же в равностороннем шестиугольнике ABCDEF равны четыре неглавные диагонали АС, СЕ, ЕА и BD (рис. 135), то этот шестиугольник правильный. Действительно, углы шестиугольника при вершинах В, С, D и F равны в силу равенства треугольников ABC, BCD, CDE и EFA (по трем сторонам), а углы при вершинах С, Е и А также равны, поскольку они представляют собой одинаковые суммы углов (один из которых есть угол при вершинах С, Е или А равностороннего треугольника АСЕ, а два других являются углами при основаниях одинаковых равнобедренных треугольников АВСУ CDE или EFA). Таким образом, все углы равностороннего шестиугольника ABCDEF равны; следовательно, он правильный.

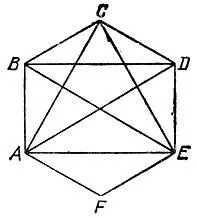
Рис. 135

Книга подходит к концу. И если до сих пор к каждой задаче давалось достаточно подробное решение, то в настоящем параграфе вам представляется возможность решать задачи в большей степени самостоятельно.

Некоторые из предложенных ниже задач, возможно, покажутся вам слишком простыми, но и в таких случаях советуем не торопиться с ответом - можно попасть впросак. Приведенные решения в большинстве случаев очень кратки, они скорее напоминают указания к решениям. Вдумчивому читателю было бы полезно попробовать доказать самостоятельно сформулированные нами утверждения.

Большинство ситуаций, описанных в настоящем параграфе, встречаются в повседневной жизни и являются естественными. Однако для своего разрешения они порой требуют некоторой изобретательности и смекалки - этим и объясняется название параграфа.

19.1. Экономный счетУ продавца в киоске конверты сложены в пачки по 100 штук. Как ему быстрее отсчитать 75 конвертов?

19.2. Стопка бумагиКак можно быстро определить примерное количество листов бумаги, содержащихся в данной большой стопке?

19.3. Множественная регистрацияВам нужно обработать огромную стопку анкет, каждая из которых содержит по несколько пунктов. Как нужно организовать одновременный подсчет тех или иных анкетных данных, чтобы, просмотрев всю стопку только один раз, можно было выдать исчерпывающую статистику по интересующим вас вопросам?

19.4. Гвозди в ящикеКак приблизительно сосчитать число гвоздей в ящике?

19.5. День отъезда - день приездаВы уехали в командировку 24 марта, а вернулись 31 марта. Сколько дней вы были в командировке?

19.6. Перекладывание конфетВ двух пакетах лежат конфеты, причем в одном пакете на 10 конфет больше, чем в другом. Сколько конфет нужно переложить из одного пакета в другой, чтобы в них конфет стало поровну?

19.7. Заготовка дровИз трехметровых и четырехметровых бревен одинаковой толщины нужно заготовить машину дров, распилив бревна на куски длиной по одному метру. Какие бревна выгоднее пилить?

19.8. Пешком по ступенямВо сколько раз путь по лестнице на 16-й этаж дома длиннее пути на 4-й этаж?

19.9. Как разыскать нужную квартируВ одном из подъездов шестнадцатиэтажного дома на первом этаже находятся квартиры с номерами 65, 66, 67 и 68. В каком подъезде и на каком этаже находится квартира с номером 165?

19.10. Пирожок без бульонаНаходясь в столовой, вы прочитали в меню, что порция бульона с пирожком стоит 31 копейку, а половина порции бульона с пирожком стоит 23 копейки. Сколько стоит пирожок?

19.11. Сдавая посудуВ буфете продается лимонад в бутылках стоимостью 30 копеек. Пустую бутылку можно вернуть, получив за нее 20 копеек. Какое наибольшее количество лимонада можно выпить, имея при себе 1 рубль?

19.12. В единую цепьЧетыре обрывка цепи, содержащих по 2 звена каждый, нужно соединить в одну цепь. Можно ли это сделать, расклепав, а затем снова заклепав меньше, чем три звена?

19.13. Общий сейфТри инженера имеют общий сейф. Как запереть этот сейф, чтобы' открывать его можно было только при одновременном присутствии или при согласии всех трех инженеров?

19.14. Общая лодкаТри рыбака имеют общую лодку, и у каждого из них есть свой замок и ключ к нему. Как прицепить лодку к берегу, чтобы любой из рыбаков мог ее отцепить с помощью одного только своего ключа.

19.15. Подбор ключейВы рассыпали связку из 10 ключей от 10 дверей. Каждый ключ подходит только к одной двери. Как за наименьшее число попыток восстановить соответствие между ключами и дверями?