Марат Авдыев - Восхождение к вершине гиперкуба. Великая теорема Ферма для миллиардов обычных людей

Чтобы найти ответ надо просто разделить все имеющиеся 7 книг на три подгруппы А, Б, В и мысленно осуществлять перестановки в каждой, их число будет

А) Всего в библиотеке 7 книг или 7! перестановок

Б) Дома у Артура 3 книги или 3! перестановок

В) Осталось в библиотеке 4 книги или 4! перестановок.

при этом не различимы варианты, когда книги остаются в пределах любой из подгрупп: не важно в каком порядке они следуют на полке дома у Артура или остаются стоять в библиотеке. Поэтому имеем:

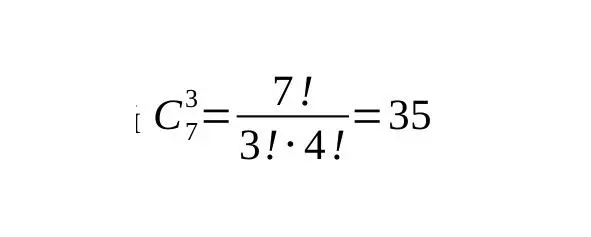
Число сочетаний для случая буккросинга на полке дома Артура

а общая формула для расчёта числа сочетаний:

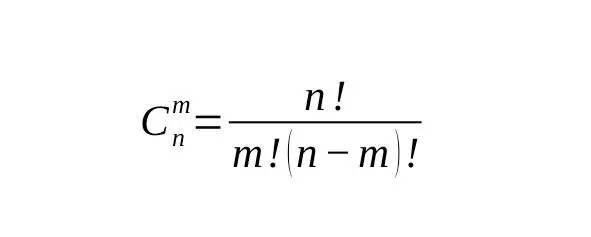
Биноминальный коэффициент или число сочетаний рассчитывается по это формуле

Смысл формулы заключается в том, что из возможных перестановок книг, перестановки на самой полке библиотеки буккросинга и личной полке читателя не имеют значения: такие перестановки рассматриваются как равнозначные сочетания. Следовательно общее число перестановок необходимо разделить на число перестановок на библиотечной полке и разделить также на число перестановок на читательской полке.

Число сочетаний это также биноминальный коэффициент . Происходит это наименование из Бинома Ньютона. Несложно раскрыть следующее выражения (a + b) nдля случая n = 2, n = 3, n = 4 – легко убедиться, что образуется ряд в виде суммы произведений вида:

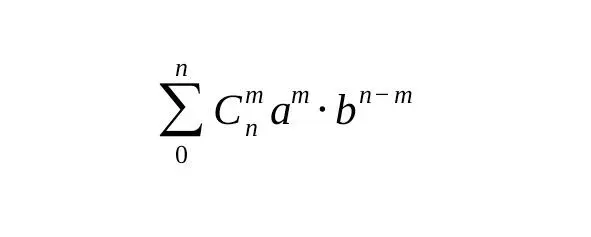
Бином Ньютона. С помощью этой формулы можно разложить выражение (a + b) n

здесь знак суммирования обозначается греческой буквой ∑, читается как сигма ,

где целое m – это счетчик, пробегающий значения от 0 до n.

Треугольником Паскаля называется треугольная таблица, в которой на вершине и по боковым сторонам расположены единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в строке выше (мысленно следует записать ещё по единице слева и справа самой верхней единицы):

1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

Как легко убедиться в каждом ряду стоит число сочетаний C n mили биноминальный коэффициент.

Любопытно разложение: (1+1) n = ∑ C n m

означающая, что сумма любого ряда всех биноминальных коэффициентов равна 2 nнапример 1 +2 +1 = 2 2 – проверьте для более высоких степеней!

=========================

Родители и Артур взяли на прокат коньки и пошли на ледовый каток. Играла музыка, из-подо льда мигала светодиодная подсветка причудливыми узорами, играла приятная мелодия. Татьяна, Матвей и Борщов предпочли конькам лыжи. Они выбрали трассу Пятёрка – пять километров в хвойном лесу, где были такие причудливые холмы с неожиданными спусками и подъёмами.

Борщов шёл коньковым ходом впереди, плавно, легко, широкими шагами, вслед за ним плавно как на коньках следовала Татьяна, замыкал этот командный забег Матвей, часто семенящий на лыжах.

Борщов сделал небольшой круг, разворот и снова оказался позади Матвея.

– Дружище, надо бы толкаться плавнее, чтобы работали руки и пресс, – показал он Матвею. – Палочка ставится плавно чуть вперёд в сторону движения, корпус догоняет её и работает рука. Плавно налегаем. Ноги пружинят. В результате работа от приложения мускульных усилий преобразуется в кинетическую энергию. Все фазы движения должны быть согласованы.

– Я за этим не успеваю следить! – ответил Матвей.

– А следить и не надо – надо чтобы красота движения была отработана до автоматизма. Красота – это значит эффективное движение, это принцип наименьшего действия, есть такой в физике… И главное, ощущение хорошей внутренней игры, как говаривал старина Тимоти Голви!

На двадцать шестой минуте группа подошла к финишу.

– Неплохо, отметила Татьяна, – а давайте сдадим лыжи в прокат и посидим в кафе на лыжной базе, пока наши фигуристы катаются на коньках.

Вся дружная компания прошла в кафе «Локомотив». Заказали чай и пирог с яблоками.

– Ну как продвигается дела с Великой Теоремой? – спросил профессор Борщов.

– Честно говоря, я даже не хотел идти на лыжах – ответил Матвей. – Все мои идеи оказались провальными. Я перепробовал пирамиды, квадратичную и другие системы координат, гиперцилиндры, гиперконусы и гиперкруги , но это заводило меня в такие дебри ….

Борщов понимающе кивал: дескать, ничего страшного, так оно и бывает. И рассказал анекдот Юрия Никулина о том, как в самолёте первым классом летела команда моряков. Все во главе с капитаном дружно уснули. И только бодрствовал попугай, который, сидя на спинке кресла капитана, снова и снова повторял: пр-р-ропали мы, пр-р-ропали! Скорчив гримасу Борщов рассказал этот анекдот, что называется «в лицах». Все дружно рассмеялись и напряжение исчезло. Еще продолжая смеяться, Матвей продолжил:

– Но вчера, складывая вещи в рюкзак, я заметил, как укладывается шарф под крышкой рюкзака. Она у меня напоминает усечённую пирамиду. Я подумал, что слои большого должны последовательно, без единого пропуска, уместиться в малом кубе целое число раз, чтобы не нарушить принцип симметрии фигуры.

– Ты имеешь ввиду, что слой или несколько слоёв из большого должен уместиться в малом кубе? – уточнила Татьяна. – Но ведь там просто нет свободного места. И вообще, что значит перемещать слои ?

– Я предлагаю зафиксировать ребра вложенных друг в друга гиперкубов a, b, c и наполнить всю эту фигуру несжимаемыми гиперкубиками, затем опустошить a-Малый гиперкуб. – Матвей достал несложный чертёж, уже хорошо всем знакомый.

– А эта стрелка, надо полагать, обозначает перемещение слоя? – спросил Борщов.

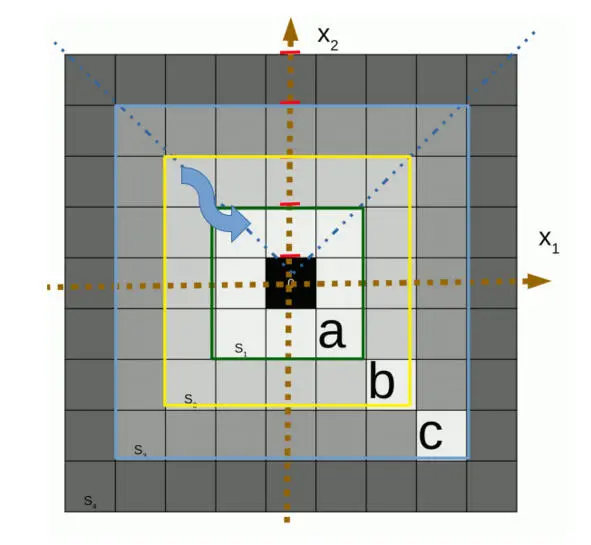
Рис. 3.1. Перемещение слоёв в гиперкубе.

– Да, и если вспомнить, формулировку Теоремы Ферма в геометрической форме, то объемы а-Малого гиперкуба должны быть равны разнице объемов между с-Большим и b-Средним гиперкубами. Я думаю, что они должны быть равны послойно.

– Почему?

– Потому что, в противном случае от перемещения слоёв будут нарушены фундаментальные свойства нашей фигуры: непрерывность и симметричность , а также принцип изотропности пространства.