Марат Авдыев - Восхождение к вершине гиперкуба. Великая теорема Ферма для миллиардов обычных людей

– Или просто ящички, ставленные в другие ящички как русская матрёшка – уточнила Татьяна.

– Да – с радостью поддержал её Матвей.

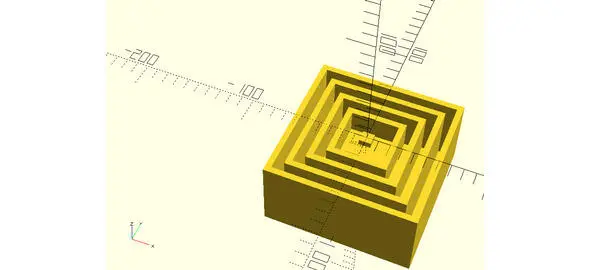
Рис. 2.3. Сечение (пронзание) трёхмерного куба двумерной плоскостью. Между слоями сделан единичной толщины сделан зазор, также равный единице, для наглядности.

– А что такое многомерный куб? – вдруг спросил Матвея Борщов.

– Ах, да! -воскликнул, Матвей, – я должен был это рассказать с самого начала. Он взял чистый лист и стал чертить: Точка, отрезок длиной а, квадрат а 2, трёх мерный куб а 3 тессеракт a 4и т. д. – это гиперкубы соответственно нольмерного, одномерного, двумерного, трёхмерного, четырёх мерного пространства… В этом ряду каждая следующая фигура размерности n образуется путем перемещения гиперкуба размерности n-1 на длину ребра а в направлении, поперечном каждому из n -1 других.

Представьте себе, что мы объясняем двумерному существу, живущему на плоскости, как можно двигаться вверх и вниз. Это конечно, трудно, но например возьмём вот эту прокладку для обуви, – и Матвей как фокусник извлёк из под стола две новые обувные стельки, завёрнутые в полиэтилен, распечатал упаковку.

– Я могу убедить математика, живущего на плоскости, что если бы он смог прибегнуть к помощи трехмерного пространства, то без труда заменил бы левую стельку правой и наоборот. А для нас, трёхмерных существ, так можно было бы поступить с ботинками, а именной взять левый ботинок перевернуть его в четырёхмерном пространстве и получить правый и опять же наоборот из правого -левый!

– Я об этом где-то читал в детстве, – задумчиво заметил Борщов.

– Но ведь пространство больше трёх, ну может быть ещё четырехмерное с добавлением оси времени, – задумчиво сказал вслух Татьяна, – словом такие фигуры существуют лишь в нашем воображении, они выдуманные, а не реальные

– А реальны ли отрицательные числа? А комплексные числа? – вдруг спросил Борщов. Матвей приготовился ответить, но Борщов кивком головы дал ему понять: позвольте мне, коллеги, это быстро объяснить простыми словами. – Отрицательные числа используется в финансах и бухгалтерии, без них невозможна работа рыночной экономики, то есть мы сопоставляем отрицательным числам реальные объекты: банковский кредит, налоги и так далее. Что касается комплексных чисел, то они упрощают работу с радиоволнами, оптикой. У каждого из Вас мобильник – это реальность? Безусловно. Что касается физических формул, то в них используются пятые, шестые и более высокие степени, аналогичная ситуация в социологии, маркетинге – другими словами, гиперкубы моделируют материальные объекты. Продолжайте, пожалуйста, Матвей.

И Матвей продолжал:

– Гиперкуб обладает свойством симметрии. Если расположить начало координат в центре гиперкуба, то каждая его вершина будет находится на расстоянии половина ребра a умножить на квадратный корень √n, что легко вычисляется по теореме Пифагора. Перпендикуляр, опущенный из центра гиперкуба на любую его грань, проходит через её центр и длина образуемого отрезка (высоты любой из совершенно одинаковых из 2n гиперпирамид, на которые рассекается гиперкуб составляет половину ребра гиперкуба ½а). Легко убедиться, что грань гиперкуба – это гиперкуб размерности на единицу меньше…

– А я видел фильм про гиперкуб! – вдруг перебил его Артур. -Там он как- то странно крутился на шарнирах…

– Да, это тессеракт , – подтвердил Матвей или четырехмерный гиперкуб, но его показывают с эффектом параллакса или о степенях выше трёх мы ещё поговорим, а пока достаточно сравнить двухмерный, он показал на шахматную доску и трёхмерный случаи, и он коснулся фигуры из деревянных кубиков.

Давайте рассечем нашу фигуру из трёх вложенных друг в друга гиперкубов на равные гиперпирамиды, конкретно квадраты мы рассечем прямыми линиями на четыре треугольника, а кубы – на шесть совершенно одинаковых пирамид, как раз по числу граней.

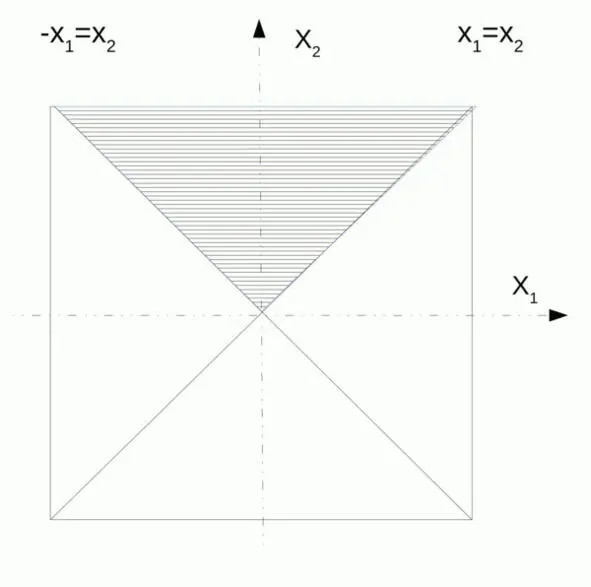
Рис. 2.4. Рассечение гиперкуба. Случай двумерного пространства. Обратите внимание на уравнения x 2= x 1или привычнее y = x – это линяя под углом 45 градусов или биссектриса угла. Подумайте, как будут расположены точки на прямой, описываемой уравнением x 2 =-x 1

– А почему они будут одинаковы? – задумчиво спросил Борщов.

– Потому что каждая пирамида имеет одинаковую высоту, равную как раз половине ребра гиперперкуба и основания каждой пирамиды одновременно являются гранями гиперкуба, а в силу симметрии грани между собой конгруэнтны, проще говоря равны. Более того эти пирамиды правильные, их грани равны и боковые ребра равны, поскольку являются полудиагоналями гиперкуба, что составляет a * √n /2.

– Ага, вижу ….

Рис. 2.5. Рассечение гиперкуба. Случай трёхмерного пространства.

– Матвей, ты хочешь сказать, что эти пирамиды также вписаны друг в друга: большая, малая и средняя? – спросила его Татьяна.

– Да, они также вписаны как и гиперкубы, но я их не стал изображать, чтобы не затруднить восприятие.

– Я кажется догадалась, ты сейчас расскажешь нам о симметрии! – предвосхитила с улыбкой Татьяна.

– Совершенно точно! – ответил Матвей. Все, что касается соотношения объёмов гиперкубов повторяется и для этих пирамид, но в силу симметрии мы можем сфокусироваться лишь на одной пирамиде, если хотите, называйте гиперпирамиде, но первое проще…

– Матвей, вдруг заговорил после небольшой паузы Борщов, – если Вы всё-таки склоняется нас в пользу геометрической наглядности, то не могли бы Вы сформулировать и саму Великую теорему в геометрической форме?

– С радостью! – ответил Матвей. Он перелистнул пару листов и наконец с расстановкой зачитал:

+++++++++++++++++++++++++++++++++++++++++++++++++++++++

В n-мерном пространстве объем a-Малого гиперкуба (объединение 1 nи последовательное наращивание k слоёв) прибавить объем b-Среднего гиперкуба (наращивание ещё l слоёв) образует объем c-Большого гиперкуба (ещё m слоёв). Ребра гиперкубов – целые числа. Все слои следуют последовательно и непрерывно, пронумерованы натуральными числами. Чтобы правая и левая часть уравнения Ферма были равны, необходимо соблюдение ряда условий: