Лев Генденштейн - Алиса в стране математики

Впереди Алисы семенили, неся торт, восемь маленьких пешек. Торт, конечно, остался шоколадным, но, увы — он перестал быть огромным! Подходя к дому, Алиса даже засомневалась: прилично ли с таким тортом приходить к чаю без приглашения? И тут она услышала грохот бьющейся посуды.

— Стоит ли вообще туда идти? — подумала Алиса, но было уже поздно: пешки-поварята входили в ворота, и Алиса поняла, что её ждут новые приключения.

Каких только обидных названий не давали отрицательным числам — их называли и нелепыми, и ложными, и придуманными... Просто удивительно, что после всего этого отрицательные числа продолжают верно служить людям!

Впервые отрицательные числа появились в Китае около двух тысяч лет назад — тогда ими пользовались для обозначения долгов (помните «минус один торт»?). Ту же роль отрицательные числа играли в Индии начиная с V —VI веков, а позднее — в средневековой Европе. Но учёные таких чисел не признавали: они считали, что «меньше чем ничто» ничего быть не может!

Однако отрицательные числа «перехитрили» математиков: они выросли внутри самой математики! Вот как это произошло.

С давних пор математики решали уравнения. Уравнение — это равенство, в которое входит неизвестная величина (такой величиной может быть, например, площадь поля, возраст человека или число рабов). Решить уравнение — значит узнать, какому числу равна эта неизвестная величина. И вот, когда это число находили, оказывалось иногда, что оно должно быть меньше нуля! Такие решения уравнений считали «ложными», «нелепыми» и отбрасывали их — действительно, разве может, например, площадь поля быть меньше нуля?

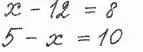
Это два уравнения, в которых неизвестное обозначено буквой x . У одного из этих уравнений решение положительное, а у другого — отрицательное

Однако скоро обнаружилось, что даже для того, чтобы получать положительные, вполне «законные» решения, приходится порой пользоваться отрицательными числами в промежуточных вычислениях, как бы на черновике. И эти «нелепые» числа надёжно приводили к правильным результатам, но... при одном удивительном условии: произведение двух отрицательных чисел надо было считать числом положительным ! Это казалось настолько странным, что один учёный назвал отрицательные числа «порождением дьявола», а другой заявил, что понять правило умножения отрицательных чисел выше человеческого разумения! В течение нескольких веков математики, скрепя сердце, пользовались отрицательными числами, но признавать их настоящими числами отказывались наотрез.

Признание отрицательных чисел пришло с неожиданной стороны.

В XVII веке жил французский учёный Декарт (во Франции ему, к сожалению, довелось жить очень мало, а книги его во Франции были запрещены). В те времена математика состояла как бы из нескольких отдельных наук: арифметики , которая изучала свойства чисел, алгебры — науки о решении уравнений, и геометрии , где изучались свойства фигур. Кроме того, следуя древним, к математике относили ещё астрономию и музыку!

И вот Декарт задался дерзкой целью: создать науку, которая объединит всю математику. «К области математики, — писал Декарт, — относятся те науки, в которых рассматриваются либо порядок, либо мера, и не имеет значения — будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое... Должна существовать общая наука, объясняющая всё, что относится к порядку и мере... и эта наука должна называться всеобщей математикой».

Основная идея Декарта была гениально проста. Он взял прямую, обозначил на ней точку и написал рядом с ней число «нуль». Затем он взял отрезок определенной длины и стал откладывать этот отрезок, как «единичную меру», вдоль прямой вправо от точки, обозначенной нулём. При этом на прямой появлялись точки, соответствующие числам 1, 2, 3... — эти числа показывали, сколько раз отложен «единичный отрезок» (помните число королевских шагов?). Теперь каждому натуральному числу соответствовала точка на прямой; это был решающий шаг — он связал числа и точки, то есть арифметику и геометрию!

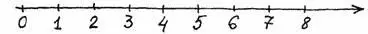
Если на прямой отметить на равных расстояниях друг от друга точки 0, 1, 2, 3 и так далее, то эта прямая превратится в числовую ось

Сделав этот шаг, Декарт догадался, что любую точку на прямой можно сопоставить с числом, и при этом точкам, расположенным на прямой левее нуля , соответствуют как раз отрицательные числа (помните числа левее нуля вдоль дороги для королевских прогулок?). Так, благодаря Декарту, отрицательные числа обрели равноправие с положительными числами и навсегда потеряли свою «нелепость».

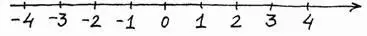
Числовая ось неограниченно продолжается в обе стороны: слева на ней расположены отрицательные числа, а справа — положительные

Точку на прямой можно задать одним числом, а для точки на плоскости нужно два числа (помните башенки с двумя числами на перекрёстках двух аллей в Китайском Саду?). Благодаря этому линии на плоскости оказалось возможным связать с уравнениями — так появились графики . О более тесной связи между алгеброй и геометрией нельзя было и мечтать: решение любой геометрической задачи можно было свести теперь к решению уравнений!

Числа, которыми обозначают точки, называют сегодня во всем мире «декартовы координаты» , хотя у Декарта были предшественники: греческий учёный Птолемей, составляя во II веке географические карты, пользовался долготой и широтой в качестве географических координат, а арабский поэт-математик Омар Хайям (о нём мы уже писали) пользовался координатами больше чем за пятьсот лет до Декарта! Одновременно с Декартом связь между алгеброй и геометрией открыл и его соотечественник Ферма. Но всё-таки название «декартовы координаты» вполне справедливо: именно Декарт развил идею о взаимосвязи разных областей математики и представил математику как единую науку, «объясняющую всё, что относится к порядку и мере».

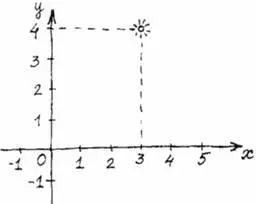
Положение любой точки на плоскости можно задать с помощью двух чисел, которые называются координатами этой точки и обозначаются обычно буквами x и y . На рисунке отмечена точка с координатами x = 3 и y = 4