Мордехай Тульчинский - Качественные задачи по физике в средней школе и не только…

Веревочка, в свою очередь, находится в равновесии. На нее действуют вес вешалки со свитером (по третьему закону Ньютона равный силе реакции веревочки, которая, в свою очередь, равна сумме сил тяжести вешалки и свитера), сила тяжести самой веревочки и сила реакции со стороны того кусочка бельевой веревки, к которому Винкель привязал веревочку с вешалкой. Из равновесия веревочки вытекает, что сила реакции со стороны бельевой веревки должна иметь такую же величину, как суммарная сила тяжести свитера, вешалки и веревочки. (Масса веревочки совсем маленькая по сравнению с массой свитера и вешалки, и в таком же соотношении находятся силы тяжести, так что веревочкой можно было бы легко пренебречь – но и особого выигрыша это нам не даст.) По третьему закону Ньютона сила реакции, действующая на веревочку со стороны бельевой веревки, по величине равна весу всей конструкции (свитера, вешалки и веревочки), действующему на бельевую веревку со стороны веревочки.

Итак, мы выстроили длинную и несколько утомительную цепочку рассуждений, которая привела нас вот к какому выводу: на кусочек бельевой веревки, к которому привязана вешалка со свитером, действует сила, по величине равная суммарной силе тяжести свитера, вешалки и веревочки. Эта сила добавляется к силам, действующим на участок бельевой веревки, которые мы проанализировали в задаче 25.

Пока Винкель не повесил вешалку со свитером на бельевую веревку, натяжение веревки уравновешивало лишь тяжесть самой веревки. Но теперь появилась дополнительная большая сила, направленная вниз. Бельевая веревка растянется, и ее середина опустится – но не сильно, если веревка натянута достаточно хорошо. Она будет по-прежнему почти горизонтальна. А значит, силы натяжения, направленные в основном вбок и лишь чуть-чуть вверх, должны стать очень большими, чтобы их вертикальная составляющая уравновесила вес свитера с вешалкой (рис. 50).

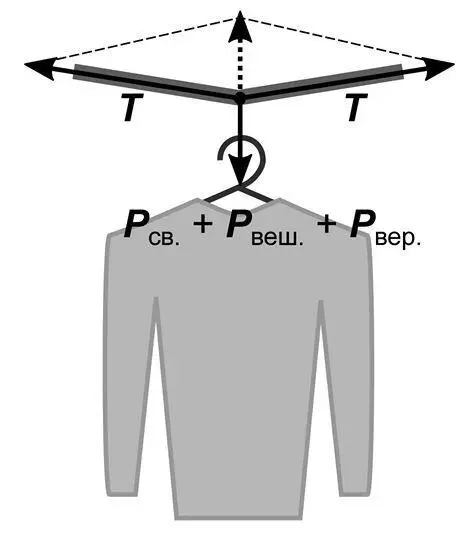
Рис. 50

Получается вот что: сила натяжения веревочки, которой привязана вешалка, по величине близка к весу вешалки со свитером. А вот прирост силы натяжения бельевой веревки многократно превосходит этот вес. Вот почему толстая и прочная горизонтальная бельевая веревка лопнула, хотя тонкая вертикальная веревочка выдержала нагрузку.

27. Цельтесь выше!

На любое летящее у земной поверхности тело действует сила земного притяжения, которая заставляет траекторию тела изогнуться – отклониться от прямой линии вниз. Для быстро летящих тел (например, для пули) это отклонение незначительно – но оно все равно есть. Именно его вы и компенсируете, поднимая прицел чуть-чуть выше нужной точки.

28. Хитрая обезьяна

Из задачи 27 мы знаем, что стрела в полете отклонится от прямой линии вниз. Однако и обезьяна за время полета стрелы сместится вниз на какое-то расстояние. Движение стрелы можно разложить на равномерное (если не учитывать сопротивление воздуха) движение в горизонтальном направлении и свободное падение под действием силы тяжести в вертикальном направлении. Все тела в поле силы тяжести падают с одинаковым ускорением – ускорением свободного падения g , поэтому по вертикали стрела и обезьяна будут смещаться с одинаковым ускорением. Это значит, что их относительная скорость будет постоянной, следовательно, стрела в момент вылета должна быть направлена точно в обезьяну.

Другой способ решения этой задачи – посмотреть на ситуацию глазами обезьяны, то есть перейти в связанную с ней систему отсчета. Эта система отсчета не будет инерциальной, потому что будет двигаться вниз с ускорением свободного падения. Такая система отсчета называется падающей, и в ней все свободно падающие тела движутся равномерно и прямолинейно. Траектория стрелы в этой системе отсчета будет прямой линией. Значит, чтобы стрела попала в цель, индеец должен целиться прямо в обезьяну.

29. Перетягивание космонавта

По закону всемирного тяготения сила тяжести не только возрастает с увеличением массы притягивающихся тел, но и убывает с ростом расстояния между ними обратно пропорционально квадрату этого расстояния. Космонавт, находящийся между Землей и Луной, испытывает притяжение со стороны обоих космических тел, и эти две притягивающие силы направлены в разные стороны. Чем ближе он к Земле, тем сильнее притяжение Земли и слабее притяжение Луны, и наоборот, чем ближе он к Луне, тем слабее притяжение Земли и сильнее притяжение Луны. Есть ли такая точка между Землей и Луной, где притяжение Луны «пересилит»?

Допустим, Земля и Луна закреплены в пространстве на расстоянии, равном среднему радиусу лунной орбиты. Нарисуем схематические графики для сил притяжения в зависимости от положения космонавта между Землей и Луной. Положение будем измерять по оси, соединяющей центры Земли и Луны и имеющей начало координат в центре Земли. По отдельности графики силы притяжения Луны и силы притяжения Земли выглядят так, как показано на рис. 51 (масштаб на графиках не соблюден).

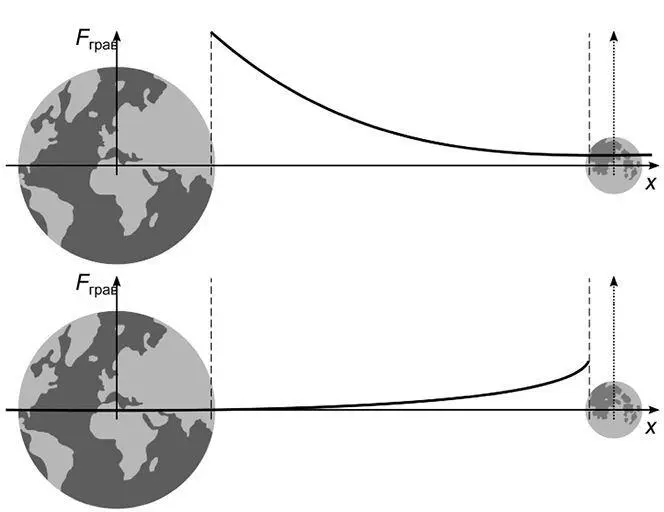
Рис. 51

При их наложении у нас могут получиться две ситуации (рис. 52).

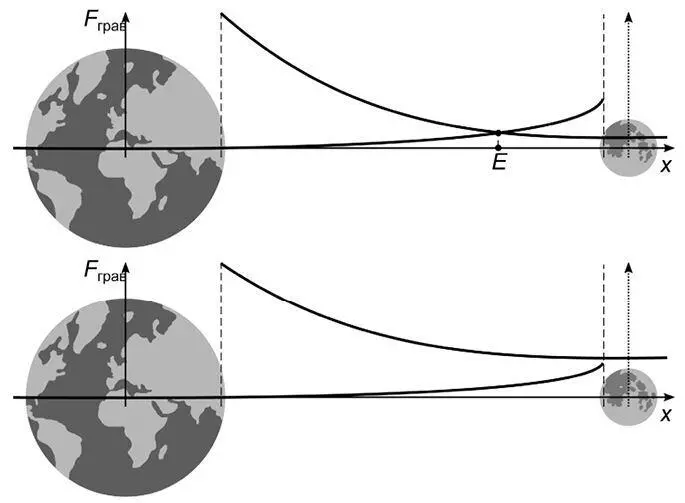
Рис. 52

Важный момент: это графики величины силы, но у силы есть еще направление, и сила притяжения Земли направлена к Земле, а сила притяжения Луны – в противоположную сторону. В первой ситуации в точке E силы притяжения уравновесят друг друга, а вблизи поверхности Луны земная сила притяжения оказывается слабее лунной. Во второй ситуации даже на лунной поверхности Земля притягивает к себе космонавта сильнее, чем Луна. (Противоположной ситуации не получится: у поверхности Земли и Земля ближе к космонавту, чем Луна, и масса Земли больше лунной, поэтому сила притяжения Луны не может оказаться больше земной.) Какая же из этих ситуаций соответствует реальности? Тут уже не обойтись без расчетов – попробуйте провести их самостоятельно, взяв справочные данные о массах космических тел и радиусе лунной орбиты и приняв массу космонавта равной 150 кг, если она вам понадобится. Можно ли так изменить массу Луны или расстояние от Луны до Земли, чтобы Земля «перетягивала» к себе космонавта даже с лунной поверхности?

А теперь самый главный вопрос (его нам могут задать более опытные сторонники «голливудской» теории): выше мы допустили, что Земля и Луна закреплены в пространстве неподвижно, однако в действительности это не так – Луна обращается вокруг Земли по орбите (а еще точнее, оба космических тела вращаются вокруг общего центра масс). Это довольно серьезное возражение, оно ставит под сомнение наши доводы. Как учет этого факта повлияет на наши рассуждения и выводы?