Мордехай Тульчинский - Качественные задачи по физике в средней школе и не только…

Черенок выступает в роли рычага. Рычаг давит на оба ящика, а ящики, по третьему закону Ньютона, ответно давят на рычаг с такими же по величине, но направленными в противоположную сторону силами.

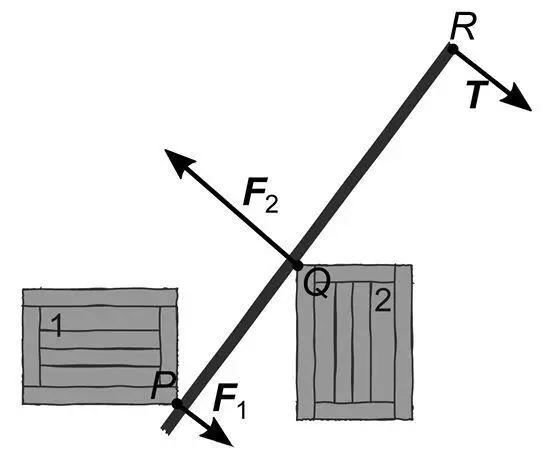
Рис. 70

Сдвинуться ящикам не дает сила трения покоя, у которой есть предельное значение. С ростом силы T пропорционально растут и силы, приложенные к ящикам. Первым сдвинется тот ящик, к которому приложена бóльшая сила. Значит, нам необходимо определить, какая сила больше: F 1 или F 2.

Допустим, опорой рычага выступает точка P . Тогда сила F 1 приложена в точке опоры, так что ее плечо равно нулю; плечо силы F 2 равно длине участка PQ ; а плечо силы T равно всей длине рычага.

Если же опорой рычага считать точку Q , то теперь уже сила F 2 приложена в точке опоры, так что ее плечо обращается в нуль; плечо силы F 1 равно длине участка PQ ; а плечо силы T равно длине участка QR . Во втором случае плечо силы T меньше, а значит, она может быть уравновешена меньшей силой – значит, сила F 1 меньше силы F 2.

К этому же выводу можно прийти, напрямую воспользовавшись вторым законом Ньютона. Пока ни один ящик не сдвинулся, рычаг находится в покое, а значит, сумма приложенных к нему сил должна быть равна нулю. При этом сила T и сила F 1 действуют в одну сторону, а сила F 2 – в противоположную. Это означает, что сила F 2 уравновешивает собой совместное действие сил T и F 1. Если T больше нуля (то есть если мы хотя бы как-то толкаем конец рычага), то F 2 должна по величине превышать силу F 1. Значит, сила F 2 первой превзойдет силу трения покоя ящика, и ящик 2 сдвинется первым.

(Перечисляя силы, действующие на черенок, мы не учли по крайней мере еще одну силу: силу тяжести. Можете ли вы объяснить, почему ее можно не рассматривать в этом анализе?)

63. Домашняя эквилибристика

Возможно, вам доводилось видеть, как падает высокое дерево (например, спиленная сосна): падение занимает несколько секунд. Проведя опыт с карандашом, вы заметите, что карандаш падает гораздо быстрее, а спичка – еще быстрее. Это позволяет выдвинуть предположение, что более длинные предметы падают медленнее, – и мы сейчас обоснуем это предположение физическими рассуждениями.

В качестве подходящей модели сосны и карандаша возьмем однородный стержень и обозначим его длину и массу буквами L и m соответственно. Падение такого стержня из вертикального положения представляет собой вращательное движение, где центром вращения выступает нижняя точка стержня, а само вращение-падение происходит под действием силы тяжести.

Вращательное движение описывается законом, очень похожим на второй закон Ньютона. Его называют основным законом динамики вращательного движения :

M = I ε, или ε = M / I .

(Чтобы увидеть аналогию, сопоставьте эту формулу со вторым законом Ньютона: F = ma , или a = F / m .) Здесь М – суммарный момент всех сил (аналог силы во втором законе Ньютона), I – момент инерции тела (аналог массы) и ε – угловое ускорение (аналог обычного ускорения).

(В полном виде это векторный закон, как и второй закон Ньютона, но мы изучаем довольно простой случай, когда вращение происходит в одной плоскости и в этой же плоскости лежит действующая на тело сила, так что можем обойтись простыми алгебраическими переменными.)

Момент силы заставляет тело вращаться с ускорением и вычисляется как произведение силы на плечо. В нашем случае падающий стержень вращается под действием силы тяжести, которая приложена к центру тяжести стержня, расположенному посередине, то есть на расстоянии половины длины стержня L от центра вращения. В тот момент, когда стержень отклонился от вертикали на угол α, момент силы тяжести будет равен 1/2 mgL sin α.

Момент инерции точечной массы равен произведению этой массы на квадрат расстояния до центра вращения, а для протяженного, «неточечного» тела вычисляется сложением моментов инерции всех его частей. Такое вычисление может быть довольно сложным вычислением, но для типичных случаев оно давно проведено и результат хорошо известен. Нас интересует момент инерции однородного стержня длины L и массы m относительно конца стержня – он равен 1/3 mL 2.

Что будет, если масса стержня увеличится, скажем, в два раза? Вдвое вырастет момент силы, но вдвое вырастет и момент инерции, а их отношение – то есть угловое ускорение – останется прежним. А что будет, если вдвое вырастет длина стержня? Момент силы увеличится в два раза, а момент инерции – в четыре , а значит, угловое ускорение вдвое уменьшится. Чем длиннее стержень, тем медленнее нарастает скорость его падения!

Таким образом, удержать на ладони длинную трость проще, чем короткую: у вас больше времени на то, чтобы отреагировать и остановить падение движением ладони. Падение карандаша происходит слишком быстро – скорости человеческой реакции не хватает, чтобы его предотвратить.

64. Как носить бревно?

Тяжесть бревна мы ощущаем по тому, как сильно бревно давит на плечо. Если на плече лежит середина бревна, обе половины уравновешивают друг друга, и мы лишь слегка придерживаем бревно рукой. Сила тяжести, действующая на бревно, уравновешивается силой, с которой плечо толкает бревно вверх. Другими словами, плечо ощущает только вес самого бревна. Если же бревно не уравновешено, то на короткий конец приходится дополнительно надавливать рукой вниз, чтобы уравновесить более длинный конец. Теперь сила, с которой плечо толкает бревно вверх, уравновешивает не только вес бревна, но и силу, с которой рука давит на бревно вниз. Бревно кажется более тяжелым.

65. Блок и рычаг

Вес груза, подвешенного на конце перекинутой через блок веревки, передается на второй конец троса. Поскольку масса груза на конце рычага вчетверо меньше массы подвешенного груза, то и его вес будет вчетверо меньше. Пользуясь правилом рычага, делаем вывод, что трос должен быть привязан к рычагу на расстоянии четверти длины от шарнира.

В этом рассуждении мы неявно сделали два предположения: в оси блока нет трения, а сам рычаг невесомый. Как повлияет на ответ вес рычага? А наличие трения в блоке?

66. Воздух ищет выход

По мере того как бутылка заполняется жидкостью, для воздуха остается все меньше места – он должен выходить. Если воронка приподнята, между носиком воронки и горлышком бутылки образуется зазор, в который воздух беспрепятственно выходит. В противном случае он будет пытаться выйти через воронку – жидкость будет булькать, литься медленно и неравномерно.