Михаил Гершензон - Головоломки профессора Головоломки. Сборник загадок, фокусов и занимательных задач
- Название:Головоломки профессора Головоломки. Сборник загадок, фокусов и занимательных задач
- Автор:
- Жанр:
- Издательство:Литагент АСТ
- Год:2017
- Город:Москва
- ISBN:978-5-17-096810-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Михаил Гершензон - Головоломки профессора Головоломки. Сборник загадок, фокусов и занимательных задач краткое содержание
Головоломки М.А. Гершензона разнообразны и необычны – это рисунки-лабиринты, оптические иллюзии, загадки по принципу оригами, фокусы, шутки, задания на логику и внимательность. Каждый сможет найти интересную для себя задачу и придумать свое оригинальное решение! Примерьте на себя роль веселого художника или всезнайки, придумавшего собственные загадки, найдите несоответствия и ошибки в обычных художественных текстах, поразмышляйте над головоломками и задачами.
Головоломки профессора Головоломки. Сборник загадок, фокусов и занимательных задач - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
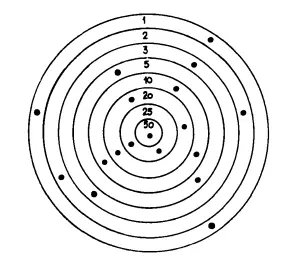
Ни одна пуля не пролетела мимо мишени.
Кто куда попал?
Мое открытие
Недавно я опоздал к поезду, и мне пришлось ждать следующего. Со скуки я нарисовал в тетрадке кружок, похожий на часы.
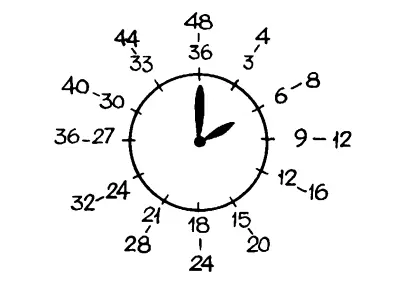
Там, где должен быть час, я написал 3, а потом на каждом следующем делении я писал ближайшее кратное трем: 6, 9, 12 и т. д. А когда этот круг чисел был готов, я рядом с ним написал второй ряд чисел, кратных четырем: 4, 8, 12 и т. д. и тоже начал с деления, на которое указывает часовая стрелка в час дня.
И тут я вдруг сделал удивительное открытие.
Если у каждого деления из большего числа вычесть меньшее, получится правильное для этого деления число часов. А если эту разность прибавить к большему числу, получится правильное для этого деления число минут!
Удивительный случай
12345679 × 9 = 111 111 111
12345679 × 18 = 222 222 222
12345679 × 27 = 333 333 333
12345679 × 36 = 444 444 444
12345679 × 45 = 555 555 555
12345679 × 54 = 666 666 666
12345679 × 63 = 777 777 777
12345679 × 72 = 888 888 888
12345679 × 81 = 999 999 999


Удивительный квадрат
Мой товарищ нарисовал на листочке бумаги картинку.
– Это удивительный квадрат, – сказал он мне. – Его придумали китайские ученые три тысячелетия назад.
– А что тут удивительного? – спросил я.
– Об этом ты сам догадайся, – ответил товарищ.

Как ни кинь – 66!
Это очень ловко построенный магический квадрат. Любой ряд, даже смежные четыре клетки в сумме дают 66! Попробуй, посчитай, сколькими разными способами ты сможешь в этом квадрате получить 66.
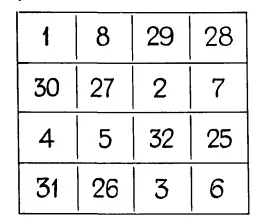
74 и 111
Это пустопорожний чудесный квадрат. Видишь, сколько в нем пустых клеток? А все-таки он чудесный: сейчас в нем любой ряд в сумме дает 74.
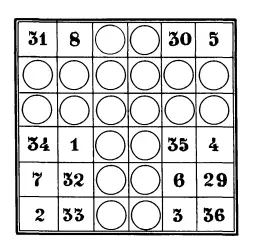
Вот и попробуй теперь вписать в пустые клетки такие числа, чтобы сумма в любом ряду была 111.
Чудесный куб
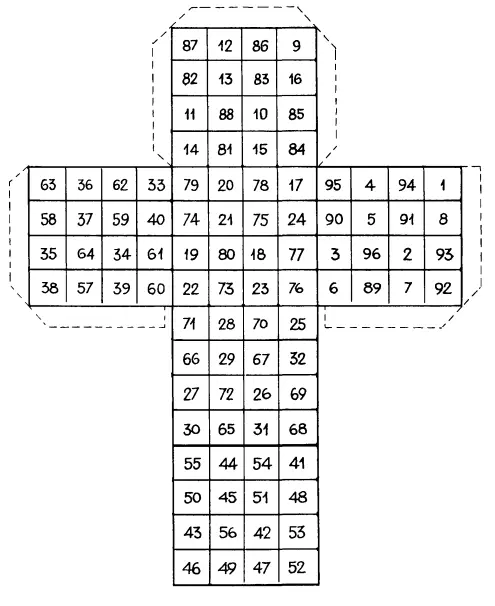
Вычерти на плотной бумаге фигуру, изображенную здесь, перепиши очень точно числа, написанные в клетках, потом вырежь фигуру и склей кубик.
Ты получишь чудесный куб, в котором с любой стороны любой ряд чисел, – слева направо, сверху вниз, наискось из угла в угол, – в сумме даст 194. Ни одно число не повторяется на этих квадратах.
Когда куб у тебя будет готов, ты можешь проделать такую штуку.
Возьми любую книгу, посмотри первую строчку на девятой странице; из этой строчки возьми четвертое слово и запиши его на бумажке; дай товарищу спрятать в карман эту бумажку, не читая конечно. Потом покажи ему свой куб и предложи сложить числа любого ряда; пусть он это сделает про себя. Тогда дай ему свою книгу и скажи, что первая цифра его суммы обозначает строку, вторая – страницу, третья – слово из этой строки на этой странице.
Он найдет это слово и будет очень удивлен, когда окажется, что это же слово написано на бумажке, которая лежит у него в кармане; он ведь не знает, что это не простой, а волшебный куб, и сумма чисел любого ряда в нем равна 194!
Еще один
– Опять чудесный? Опять магический? Опять квадрат?
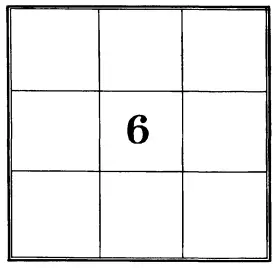
– Ну да. Ты ведь знаешь, что я их люблю. Вот впиши в пустые клетки числа, да так, чтобы сумма в верхних двух рядах, и в обоих боковых, и по двум большим диагоналям, и по четырем малым диагоналям – всюду была 18. И еще, чтобы в каждой клетке были другие цифры!
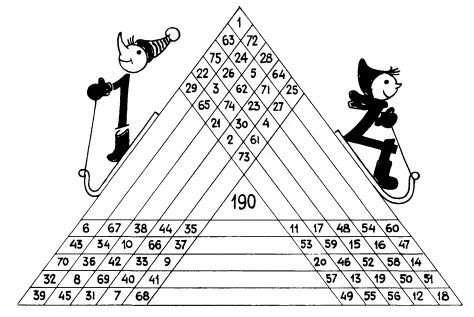
Покатайся с этой горки
Посчитай, на скольких дорожках числа в сумме дают 190.
Ответы
Надя нашла 2 гриба – два подосиновика: один сразу нашла, а другой потом. Больше она ничего не нашла.
Таня нашла вдвое больше – 4 гриба.
Лена нашла вдвое больше, чем Таня, – 8 грибов.
А ведь Лена собрала столько, сколько Мишка с Петей вместе. Значит, Мишка с Петей вместе нашли 8 грибов.
Ни Мишка, ни Петя не могли быть в паре с Леной, потому что в каждой паре мальчик нашел на 1 гриб больше, чем девочка. Значит, Лена была в паре с Колей Кочерыжкиным и Коля нашел 9 грибов!
Ура! С одной парой покончили!
Остались Надя, Таня, Мишка и Петя. Кто же из них с кем был в паре?
Мишка с Петей вместе нашли 8 грибов, Надя – 2, а Таня – 4. Значит, один из мальчиков нашел 3 гриба (на один больше Нади), а другой – 5 (на один больше Тани)
Кто же нашел 3, кто 5?
Тут нужно вспомнить, что Мишка с Колей нашли столько грибов, сколько Лена и Таня вместе.
А Лена и Таня нашли 8 и 4, то есть 12 грибов.
Про Колю мы уже знаем: он нашел 9 грибов
Значит, Мишка нашел 12 без 9, то есть 3 гриба.
Вот и отгадали, что Мишка был в паре с Надей, а Петя – с Таней.
Лена подумала, подумала и догадалась.
– Ага, – говорит, – поняла! К тому времени, как вы встретились с товарищами по несчастью, вы успели вдевятером съесть однодневный запас У вас осталось уже только на четыре дня продуктов. А как прибавились новые ребята – оказалось, что запаса только на три дня.
– Правильно, – кивнул Сергеев.
– Ну, вот и выходит, что второй группе на три дня нужно было столько же продуктов, сколько вы, девятеро, съели бы за один день. Значит, новеньких было трое.
– Молодец, Лена! – сказал Сергеев. – Конечно, их было трое. На будущий год непременно возьму тебя в экспедицию. Будешь у нас завхозом.
Лакомкин арбуз был вчетверо длиннее, вчетверо толще и вчетверо выше, чем Сережин. Значит, по своему объему он был 4 × 4 × 4, то есть в 64 раза больше Сережиного арбуза. А Костин арбуз был вдвое длиннее, вдвое толще и вдвое выше, чем Сережин. Значит, по своему объему он был 2 × 2 × 2, то есть в 8 раз больше Сережиного. Выходит, что дома Лакомка проглотил 64 таких арбуза, как Сережин, а при ребятах 8 + 1, то есть 9 таких арбузов. Значит, всего 73. Потому что все они были и красные и сладкие.
Читать дальшеИнтервал:
Закладка:










