Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Внутри – красный додекаэдр, он вырастает в белый икосаэдр, а тот опять вырастает в додекаэдр, показанный синим цветом.

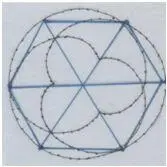
Рис. автора.

Фигура, которая образуется, когда завязываешь узел.

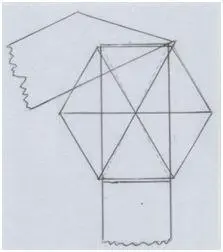
Рис. автора.

Прозрачный узел в процессе завязывания.

На первый взгляд даже трудно вообразить, что это всё – в скрипичном ключе!..

Но выходит, что в очень разных и непохожих внешне формах и явлениях можно обнаружить общую связь.

Мы всего лишь меняли точки зрения – «системы отсчёта».

Вот ещё одна точка зрения.

Что если бы мы завязали наш скрипичный ключ-узел не из плоской ленты, а из круглой верёвочки?

Чтобы завязать плоский узел, нам хватило бы шести квадратов на ленте.

Это чертёж узла.

Чтобы завязать узел из круглой верёвочки, нам хватит её длины, равной шести цилиндрическим кусочкам; при этом высота и диаметр каждого цилиндрика равны (тот же квадрат). Можешь проверить практически.

А ещё в объём этого отрезка верёвочки помещается объём девяти сфер (по закону Архимеда объём сферы, вписанной в цилиндр, равен 2/3 объёма цилиндра). 9/6 = 3/2. Квинта! Верёвочный узел тоже покажет квинту.

Но мы вернёмся к плоскости, скрипичному ключу и вращению трезвучия.

Ключ = узел.

Ключ указывает на трезвучие.

Трезвучие вращается-обращается:

1-е обращение – секстаккорд ( «секст» – «шесть», «секста» – «шестая»).

2-е обращение – квартсекстаккорд ( «кварт» – «четыре», «кварта» – «четвёртая»).

Когда мы завязываем узел, вращая ленту, первый поворот нарисует 6 в виде шестиугольника.

После следующего поворота мы продеваем ленту в петлю, и она рисует нам квадраты-кварты.

Рис. автора.

Затянутая петля превращается в пятиугольник-квинту. А в квинту заключено и трезвучие в своём начальном виде – из двух терций.

Выходит, геометрия скрипичного ключа содержит в себе намёк и на обращения трезвучия: секстаккорд и квартсекстаккорд. Удивительны свойства этого ключа!

А для чего вообще трезвучиям нужно вращаться?

А для того же, для чего вращаются электроны в атомах и все космические тела – для связи, для преобразований; для того, чтобы атомы с помощью электронов соединялись друг с другом; чтобы космические пылинки образовывали звёзды и планеты, а из них – галактики… Переменами и связью держится жизнь.

Тонические трезвучия тональностей на самом деле не прыгают по квинтам, когда ТОНАЛЬНОСТИ-актрисе захочется смодулировать – измениться. Они «подкатываются» к доминанте-квинте, чтобы утвердить на ней новую тонику.

Как это может происходить?

Если бы мы захотели запечатлеть этот процесс модуляций с помощью ключей-клавиш клавиатуры…

Впрочем, посмотри на страничках ниже. Вот что у нас получилось бы. Башня! В целых две страницы. Довольно громоздкая геометрия.

Геометрия нотной записи, конечно же, выглядит компактнее.

Рис. и пометки автора.

Две страницы (которые ниже) упаковались, сжались в две строки.

Рис. автора.

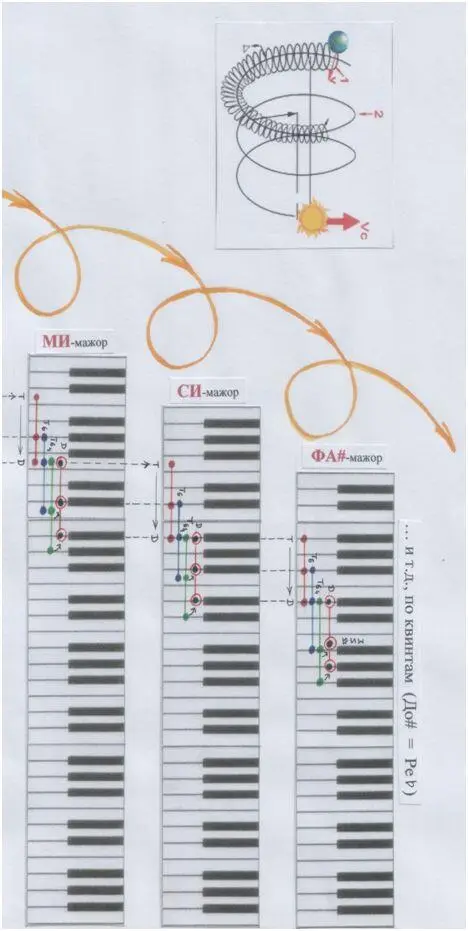
Рис. автора.

Как в данном случае происходит модуляция по квинтам?

Тоническое трезвучие, обернувшись квартсекстаккордом, оказывается на доминантном звуке (на квинте). И тут срабатывает гравитация, притяжение, «магнитное поле» доминанты. И эта доминанта перетягивает верхнюю терцию тонического квартсекстаккорда к себе поближе и превращается в новое трезвучие, с новой тоникой.

Рис. автора.

Сила притяжения звуков! Эта сила и связывает, и влечёт к переменам.

Эта сила – соль модуляций.

А гравитацию-притяжение создаёт о б щ и й з в у к (объединяющий звук).

Мы можем поиграть в модуляции по квинтам и в миноре.

Правда, в натуральном миноре доминанты будут получаться не активными, а будто вялыми, несколько печальными. Или слишком спокойными? А может быть, слишком задумчивыми, погружёнными в себя? Во всяком случае, они не вспыхивают энергией солнечных лучей.

Ты можешь воспроизвести это на клавиатуре (читая нотные знаки) и услышать в звуках.

Рис. автора.

В г а р м о н и ч е с к о м миноре всё куда интереснее! Ведь там появляется

м а ж о р н о е доминантовое трезвучие. Есть возможность вообще уйти в мажорные тональности.

А можно возвращаться к минору. И тогда мажорный «всплеск» будет похож на улыбку посреди задумчивости, на лучик надежды посреди печали, на солнечный проблеск меж облаков, на лоскуток радуги во время дождя… Ты же помнишь, что хроматизмы – это оттенки: оттенки звука – как оттенки цвета. Гармонический минор – цветной!

Рис. автора.

Круженье аккордовых звуков можно я в н о ощутить, если проиграть аккорды приёмом а р п е д ж и о (вспомнились арфа и кифара).

Ты, пожалуй, заметил, что размах (масштаб) темперированного строя никак не умещается в пространстве только скрипичного ключа.

А ничего удивительного. Темперированный строй, можно сказать, рос вместе с оргáном. Масштаб – ого!

Только подумаешь об оргáне – и тут же слышишь в себе его пронизывающие бездонные б а с ы. Пространство!

Басовый ключ явился нам так незаметно и естественно, лишь только мы пожелали прогуляться по пространству звука, по его квинтам.

Есть ли тайны у басового ключа?

Ключ «ФА».

Вот сразу покажу звуковой диапазон оргáна – нотными знаками:

Рис. из Википедии.

Конечно, как же обойтись тут без басового ключа?

Но почему этот ключ – именно «ФА» (а не тоже «СОЛЬ», что на первый взгляд кажется более удобным)?