Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

А ты помнишь то трезвучие, что явилось нам в Сфере Александера?

Вот чудо обнаружилось:

Если квинту «ДО – СОЛЬ» просчитать хроматическими звуками, то по количеству звуков она окажется о к т а в о й (до-до#-ре-ре#-ми-фа-фа#-соль – 8 звуков), а терция «ДО – МИ» окажется по количеству хроматических звуков к в и н т о й (до-до#-ре-ре#-ми – 5 звуков). Что за чудесные превращения!

Сущая головоломка!

Но – захватывающая. И уж точно – геометрическая.

Давай сделаем (умозрительно) печать звука – печать-ноту, эллипсоид: его вертикальная ось – размером от линейки стана до линейки, горизонтальная ось – чуть больше.

Пропечатаем подряд все звуки в диапазоне, который охватывает ключ «СОЛЬ» на нотном стане:

Рис. автора.

Что мы увидим?

Мы увидим, что ноты образовали восходящую линию.

Если мы измерим длину этой линии, то окажется, что эта самая длина является длиной окружности, диаметром которой является высота скрипичного ключа! Проверь сам.

(На моём настоящем рисунке высота ключа – 3,5см; длина линии нот ≈ 11см.

3,5 х 3,14 = 10,99. Ты же помнишь, что длина окружности вычисляется по формуле L=πD.)

Вот ещё как может маскироваться круженье.

Мы видим, что ноты образовали диагональ.

Ключ указывает на вертикаль, а линии нотного стана – горизонталь.

Сам собою напрашивается треугольник. Даже два треугольника.

Но мы пока поиграем-поэкспериментируем с одним.

Рис. автора.

Давай вырежем его из бумаги и накрутим на вертикаль ключа (подойдёт соломинка для коктейля диаметром с ноту на нашем рисунке).

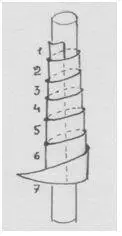
Рис. автора.

Мы увидим спираль!

Если соломинка оказалась действительно диаметром с ноту, мы увидим семь витков спирали – как семь нот гаммы (диатоники).

А ведь мы, можно сказать, закручивали диапазон октавы (от линейки до линейки, как показывает вертикаль ключа). Просто волшебство какое-то.

Есть ещё более изумительное волшебство в нашем рисунке с ключом и нотами.

Вертикаль ключа показывает нам октаву, а диагональ звуков – две октавы, укладывающиеся в октаву ключа.

Когда учёные, занимающиеся квантовой физикой (наисовременнийший раздел физики), пришли в результате своих исследований к модели пространства, они обнаружили, что само пространство обладает особой

в р а щ а т е л ь н о й с и м м е т р и е й. В этом пространстве сфера совершает полный поворот не в 360˚, а в 720˚ – то есть, поворот вдвоебольший на самом деле.

Получается, что ноты демонстрируют нам аналогичное явление.

Как это явление объясняют сами физики, ты сможешь прочитать в небольшой, но очень доступной для понимания и увлекающей своей живостью статье-эксперименте Сета Ллойда, профессора квантовомеханической инженерии (из книги Джона Брокмана «Теории всего на свете»). Статья «Истинная симметрия пространства» – на страничках ниже. А вот – цитата из статьи, об итоге эксперимента:

«…вы обнаружите, что траектория мяча походит на изображённую в пространстве восьмёрку или знак бесконечности (∞) и что траектория эта совершила не один полный поворот, а два. Таким образом, истинная симметрия пространства соответствует повороту не на 360˚, а на 720˚.»

Так выглядит начало статьи об истинной вращательной симметрии пространства. Статью полностью можно прочитать в книге.

Подобное явление можно обнаружить и в эксперименте на плоскости, с кругами: когда один круг совершает поворот вокруг своей копии (как самого себя же).

Посмотри и поэкспериментируй.

Мы экспериментируем на плоскости, которая служит нам сейчас в качестве проекции пространства (как плоские тени от объёмных предметов).

Синяя точка на рисунке отмечает начальное положение.

Когда круг А сам по себе в результате своего движения будет выглядеть так же, как он выглядит сам по себе на первом рисунке (с той же синей точкой справа), это будет означать, что он совершил поворот на 360˚ вокруг своего центра.

Начальное положение круга А:

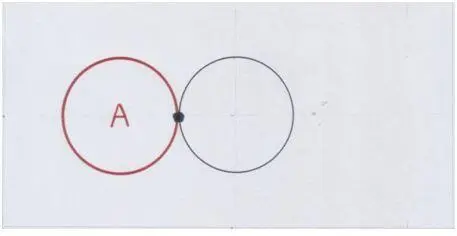
Рис. автора.

Начинаем катить круг А по линии окружности другого круга:

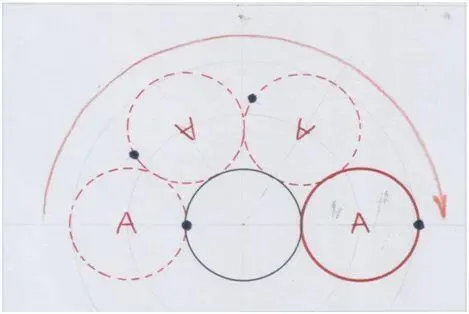
Рис. автора.

Круг А выглядит так же, как в начале своего пути. Он совершил поворот на 360˚, но в начальное положение не вернулся. Ты можешь проверить это практически, вырезав круги из картона. Ты можешь о с я з а т ь этот геометрический процесс.

Катим круг А дальше:

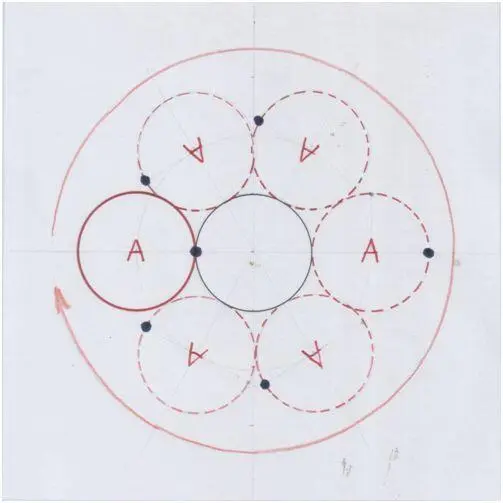
Рис. автора.

Круг А повернулся ещё на 360˚ и вернулся в начальное положение.

Итого он совершил поворот на 720˚.В этом явлении удивительно вот что:

Обе начальные окружности (чёрная и круга А) совершенно одинаковы, с одинаковым количеством точек, из которых состоят. При движении круга А все точки его окружности должны были совпасть с точками чёрной окружности «точка в точку», – допустим, на каждый градус поворота – по точке. Но градусов поворота оказалось в два раза больше, – как будто у окружности круга А и точек в два раза больше.

Подобному явлению удивлялся и немецкий математик Георг Кантор, только по поводу графиков функции. Он удивлялся тому, что количество точек отрезка равно количеству точек квадрата. Только в случае с функцией две точки координат сливаются в одну точку функции. Этот пример – из книги В.Босса «Интуиция и математика». Кантор говорил, что его рассудок отказывается это принимать, но очевидность – убедительна.

Вообще, вся эта геометрическая картинка заставила вспомнить знаменитые эпициклы Птолемея. В его космической системе планеты двигались подобным образом. Знал ли Птолемей об истинной вращательной симметрии пространства? Тогда квантовой механики ещё не было… Система Птолемея, в конце концов, была отвергнута последующими поколениями астрономов, но до сих пор даже современных учёных удивляет точность, с которой эта система предсказывала явление планет, их движение на земном небосклоне.

А теперь просто посмотри на продолжение этой геометрической игры:

Если соединить точки вращения круга А…

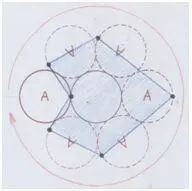
Рис. и пометки автора.