Лариса Вольницкая - Музыкальная геометрия мира: музыка и мы. Игра-эксперимент «Узел» в письмах к М.

Лист? Сердце?

А если почаще наносить точки вращения… (Ты можешь проэкспериментировать сам, с помощью кругов.)

Рис. автора.

Сердце? Яблоко?

Согласись, что музыкальная геометрия – геометрия нотного стана – выглядит намного компактнее. И весьма лаконично она даёт нам знать («нота» – «знать») об истинной вращательной симметрии пространства. К тому же – эта геометрия звучит!

На самом деле в этой тайне для нас нет ничего тайного. Нужно только суметь

у в и д е т ь некоторые отношения, пропорции в геометрии ключа – и всё!

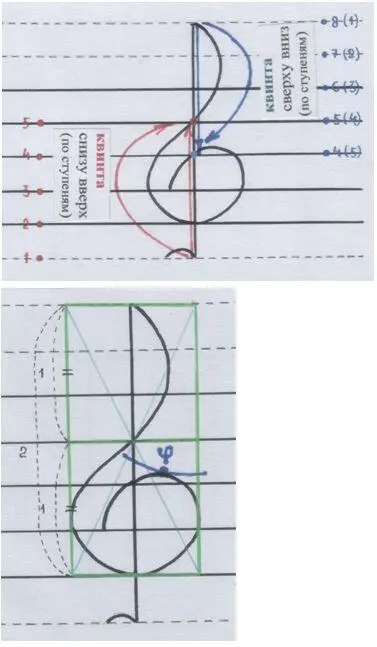
Рисунки автора.

Дальше – чуть поинтереснее. Присмотрись.

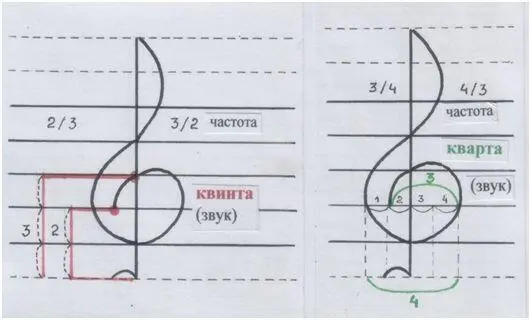
Рис. автора.

Конечная точка большого завитка может указывать и на квинту, и на кварту.

А никакого страшного противоречия нет. Мы-то хорошо знаем, что кварта – это всего лишь перевёртыш квинты: как будто её отражение в зеркале, где правое и левое меняются местами.

В конце концов, нота СОЛЬ может быть не только квинтой До-мажора, но и до-минора; может быть квартой Ре-мажора и ре-минора.

Это всего лишь говорит о великих потенциальных возможностях ключа. По опыту ты знаешь, что в с е тональности пользуются его услугами!

Так что… как посмотреть. А «как посмотреть» – это значит выбрать систему отсчёта и как и что в ней соотносить. И это – принцип относительности.

Вот! В музыке тоже действует принцип относительности.

Геометрия в пространстве.

Возьмём Геометрию за ручку и выведем прогуляться в пространство.

Мы будем с нею играть. А как же!

Пусть линия станет полоской бумаги ≈ 5мм шириной и 300мм длиной.

Раз-два-три – начало игры! Смотри и повторяй:

Рис. автора.

Совет: начинай снизу вверх, по логике звука и нотного стана. В любой игре обязательно есть логика.

Получилось?

…Результаты экспериментов принято изучать, анализировать.

И мы попробуем.

Первая петля:

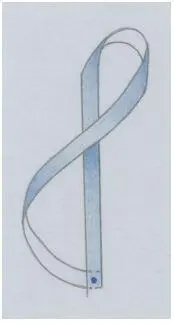
Рис. автора.

Если мы её склеим в обозначенной точке, у нас получится Петля Мёбиуса ( она же – Лента Мёбиуса). Она будет обладать свойствами Ленты Мёбиуса, даже если мы склеим концы нашей ленты под прямым углом.

Напомню свойства этой Ленты:

Непрерывность.

Парадокс: двеповерхности ленты на самом деле являются однойповерхностью для скользящего по ленте пальца. Наш палец скользит всё время в одном направлении непрерывно, не перескакивая с одной поверхности на другую, но при этом бывает на обеих поверхностях.

Два – в одном, одно – из двух. Два – как одно.

Этот парадокс удивлял и Георга Кантора в связи с графиком функции (кол-во точек квадрата из координат (а их две) то же, что и в получаемом отрезке из одиночных точек. Этот же парадокс и во вращательной симметрии пространства, и… в геометрии нотного стана.

И вот ещё сам ключ намекает на это же своей петлёй.

Тут надо приплюсовать и третье свойство Ленты (Петли) – бесконечность.

Продолжим?

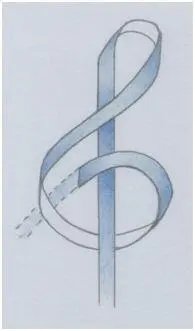
Рис. автора.

Сделай так и затяни аккуратно концы ленты.

…Моя лента совершила вращательное движение в пространстве и успокоилась на такой знакомой фигуре! Вот на этой:

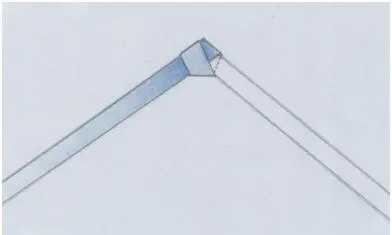
Рис. автора.

Как тебе такое?

Скрипичный ключ – зашифрованный узел?!

Выходит, что так. К тому же, узел – мы знаем – обладает свойствами Ленты Мёбиуса, когда замкнут.

Сам узел может выполнять функцию склейки в Ленте Мёбиуса. Он ведь переворачивает, меняет местами противоположности: верх-низ, лево-право.

Давай сравним ключ и свободный замкнутый узел:

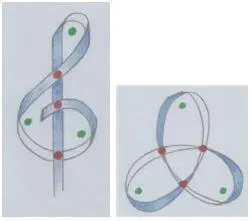
Рис. автора.

Три петли (зелёные точки). Три пересечения (красные точки).

Трезвучие.

Со второй фигурой можно играть в обращения трезвучий, если катить её, словно колесо:

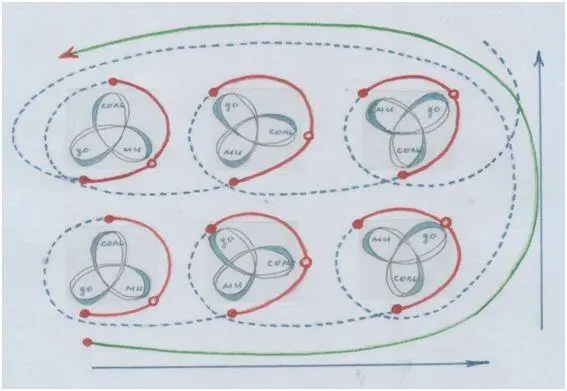
Рис. автора.

Начинаем снизу и кружимся вверх – по правилу поведения звука (обертонов); слева направо – по правилу устроения клавиатуры.

Ох, что-то это напоминает…

Движение планет и самой солнечной системы тебе это не напоминает?

А давай покатаем колесо (круг то есть). Играть так играть!

Мы это делали, когда вникали в истинную вращательную симметрию пространства. Только у нас теперь будет круг с тремя точками-нотами: ДО-МИ-СОЛЬ, трезвучие.

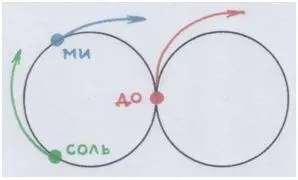
Рис. автора.

…У меня вот что получилось:

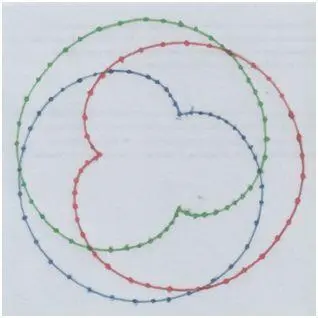
Рис. и пометки автора.

Три «кардиоиды»!

А ты можешь проверить всё сам, экспериментально. Круги в кармашке слева.

Отметь все три точки в начальном положении и продолжай отмечать, когда начнёшь катить, то есть вращать, «трезвучие». И так – пока наше трезвучие не вернётся в начальное положение.

Круговое вращение вернуло нас к петлям!

Давай поисследуем: что мы здесь интересненького разглядим?

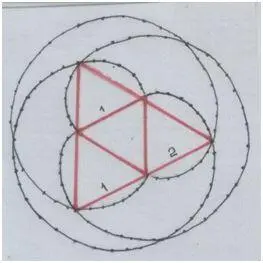
Рис. автора.

Геометрическая прогрессия (k=2, или ½).

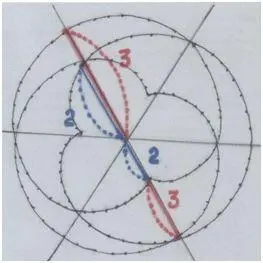
Рис. автора.

Квинтовые отношения.

Рис. и пометки автора.

Подобия с намёком на чередование.

Подобное чередование мы видели в проволочном «еже», выращенном из проволок, размеченных в соответствии с числами Фибоначчи.

Напомню:

Модель автора.