Джон Келлехер - Наука о данных. Базовый курс

При обучении без учителя алгоритм кластеризации будет искать группы строк, которые более похожи друг на друга, чем на другие строки. Каждая из этих групп определяет кластер подобных объектов. С точки зрения изучения причин развития диабета выявление кластеров схожих пациентов (объектов) может помочь выявить причины заболевания или сопутствующих диабету заболеваний путем поиска значений атрибутов, которые относительно часто встречаются в кластере. Простая идея поиска кластеров подобных объектов служит мощным инструментом и применима ко многим областям жизни. Другой пример кластеризации строк — предоставление рекомендаций для клиентов. Если клиенту понравилась книга, песня или фильм, он с высокой вероятностью получит удовольствие от другой книги, песни или фильма из того же кластера.

Прогнозирование — это задача оценки значения целевого атрибута конкретного объекта на основе значений других его атрибутов. Проблему прогнозирования решают алгоритмы машинного обучения с учителем, которые генерируют модели прогнозирования. Пример спам-фильтра, который мы использовали для иллюстрации обучения с учителем, подойдет и здесь: мы используем обучение с учителем при создании модели спам-фильтра, которая является моделью прогнозирования. Типичным случаем использования модели прогнозирования является оценка целевого атрибута для новых объектов, которых нет в наборе обучающих данных. Продолжая пример со спамом, мы обучаем спам-фильтр (модель прогнозирования) на наборе данных старых писем, а затем используем эту модель, чтобы предсказать, являются ли новые письма спамом или нет. Проблемы прогнозирования, возможно, самый популярный тип проблем, для которых используется машинное обучение, поэтому оставшаяся часть этой главы будет посвящена прогнозированию в качестве примера для введения в машинного обучения. Мы начнем наше знакомство с моделями прогнозирования с фундаментальной прогностической концепции, известной как корреляционный анализ. Затем мы покажем, как алгоритмы машинного обучения с учителем работают над созданием различных типов популярных моделей прогнозирования, в том числе моделей линейной регрессии, моделей нейронных сетей и деревьев решений.

Корреляция описывает силу взаимосвязи между двумя атрибутами. В общем смысле корреляция может описывать любой тип связи. Термин «корреляция» также имеет конкретное значение в статистике, где он часто используется как сокращенный вариант «коэффициент корреляции Пирсона». Коэффициент корреляции Пирсона измеряет силу линейных зависимостей между двумя числовыми атрибутами и находится в диапазоне значений от –1 до +1. Для его обозначения используется буква r , также называемая коэффициентом корреляции между двумя атрибутами. Коэффициент r = 0 указывает, что два атрибута независимы друг от друга. Коэффициент r = +1 указывает, что два атрибута имеют идеальную положительную корреляцию, означающую, что любое изменение одного из них сопровождается эквивалентным изменением другого в том же направлении. Коэффициент r = –1 указывает, что два атрибута имеют идеальную отрицательную корреляцию, при которой каждое изменение в одном из них сопровождается противоположным изменением в другом. Общие рекомендации по интерпретации коэффициентов корреляции Пирсона состоят в том, что значение r ≈ ± 0,7 указывает на сильную линейную зависимость между атрибутами, r ≈ ± 0,5 — на умеренную линейную зависимость, r ≈ ± 0,3 — на слабую зависимость, а r ≈ 0 — на отсутствие зависимости между атрибутами.

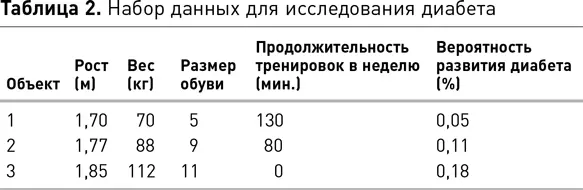
Но вернемся к исследованию диабета. Исходя из наших знаний о физиологии людей, мы ожидаем, что между некоторыми признаками в табл. 4.1 будут взаимосвязи. Например, обычно чем выше человек, тем больше размер его обуви. Мы можем ожидать, что чем больше кто-то тренируется, тем меньше в нем будет избыточного веса, с учетом того, что более высокий человек, вероятно, будет тяжелее более низкого, который тратит столько же времени на физические упражнения. Мы также ожидаем, что не обнаружим очевидной связи между размером обуви и временем тренировок. На рис. 9 представлены три диаграммы рассеяния, которые иллюстрируют, как эти интуитивные ожидания отражаются в данных. Диаграмма рассеяния вверху показывает, как распределяются данные, если они построены в зависимости от размера обуви и роста. На этой диаграмме рассеяния наблюдается четкая закономерность, идущая из нижнего левого угла в верхний правый, указывающий на то, что по мере того, как люди становятся выше (движение вправо по оси y ), размер их обуви тоже увеличивается (движение вверх по оси х ). Подобная закономерность данных в диаграмме рассеяния указывает на положительную корреляцию между двумя атрибутами. Если мы вычислим коэффициент корреляции Пирсона между размером обуви и ростом, то r составит 0,898, т. е. мы имеем сильную положительную корреляцию между этой парой атрибутов. Средняя диаграмма рассеяния показывает, как данные распределяются, когда мы строим график корреляции веса и физических упражнений. Здесь общая схема имеет противоположное направление от левого верхнего угла до нижнего правого, что указывает на отрицательную корреляцию — чем больше люди тренируются, тем меньше их вес. Коэффициент корреляции Пирсона для этой пары признаков равен r = –0,710, что указывает на сильную отрицательную корреляцию. На последнем графике рассеяния отображается корреляция времени тренировок и размера обуви. Мы видим, что данные распределены на этом графике случайным образом и коэффициент корреляции Пирсона для этой пары атрибутов r = –0,272, иначе говоря, корреляция отсутствует.

Может показаться, что применение статистического коэффициента корреляции Пирсона к анализу данных ограничено только парами атрибутов. К счастью, мы можем обойти эту проблему, применяя функции для групп атрибутов. В главе 2 мы ввели индекс массы тела (ИМТ) — отношение веса человека (в килограммах) к квадрату его роста (в квадратных метрах). ИМТ был изобретен в XIX в. бельгийским математиком Адольфом Кетле для того, чтобы задать значения для каждой из следующих категорий: люди с недостаточным весом, с нормальным, с избыточным или страдающие ожирением. Мы знаем, что вес и рост имеют положительную корреляцию (как правило, кто выше, тот и тяжелее), поэтому, поделив вес на рост, мы можем отслеживать зависимость первого от второго. Есть два аспекта ИМТ, которые представляют интерес для нашего обсуждения корреляции между несколькими атрибутами. Во-первых, ИМТ — это функция, которая принимает ряд атрибутов в качестве входных данных и сопоставляет их с новым значением. По сути, такое отображение создает новый производный атрибут (в отличие от необработанного атрибута) в данных. Во-вторых, поскольку ИМТ человека представляет собой числовое значение, мы можем рассчитать корреляцию между ним и другими атрибутами.