Джон Келлехер - Наука о данных. Базовый курс

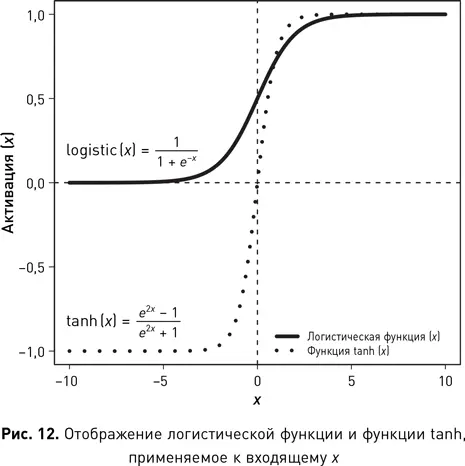
Стоит подчеркнуть, что каждый нейрон в нейронной сети выполняет очень простой набор операций:

1. Умножает каждый вход на его вес;

2. Суммирует результаты умножения;

3. Проводит этот результат через функцию активации.

Операции 1 и 2 являются просто вычислением функции регрессии с несколькими входами, а операция 3 использует функцию активации.

Все связи между нейронами в нейронной сети являются направленными, и каждая имеет свой вес. Нейрон применяет вес связи к входящему значению, которое он получает через эту связь, когда вычисляет функцию множественной входной регрессии. Рис. 13 иллюстрирует топологическую структуру простой нейронной сети. Квадраты A и B в левой части обозначают зоны памяти, которые мы используем для представления входных данных в сеть. В этих зонах обработка или преобразование данных не выполняются. Эти узлы можно считать входными или сенсорными нейронами, функция активации которых настроена таким образом, чтобы выходное значение равнялось входному [16]. Круги C, D, E и F на рисунке обозначают нейроны в сети. Бывает полезно представлять нейроны в сети организованными в слои. Сеть на рисунке имеет три слоя нейронов: входной слой содержит A и B , скрытый — C, D и E , а выходной слой содержит F . Понятие «скрытый слой» указывает на тот факт, что нейроны в этом слое не принадлежат ни входному, ни выходному слоям и в этом смысле недоступны взгляду.

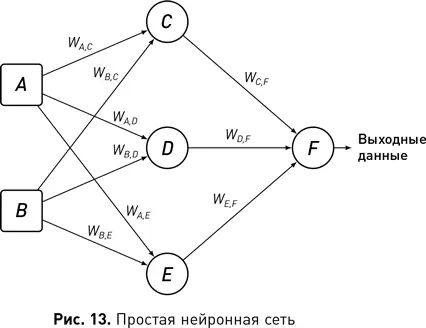
Стрелки, соединяющие нейроны в сети, обозначают поток информации. Технически данная конкретная сеть является нейронной сетью с прямой связью, поскольку в сети нет петель — все соединения направлены в одну сторону, от входа к выходу. Кроме того, эта сеть считается полностью подключенной, поскольку каждый нейрон связан со всеми нейронами в следующем слое сети. Можно создать множество различных типов нейронных сетей, изменив количество слоев, число нейронов в каждом слое, тип используемых функций активации, направление соединений между слоями и другие параметры. На самом деле разработка нейронной сети для конкретной задачи во многом сводится к экспериментам по поиску наилучшей схемы.

Метки на каждой стрелке показывают вес, который узел применяет к информации, передаваемой по этому соединению. Например, есть стрелка, соединяющая C с F , которая указывает, что выходные данные из C передаются как входные данные для F и F будет применять к ним вес.

Предположим, что нейроны в сети на рис. 13 используют функцию активации tanh. Тогда вычисление, выполняемое нейроном F , может быть представлено как:

Выходные данные = tanh (ω C,FC + ω D,FD + ω E,FE ).

Математическое представление обработки, выполняемой в нейроне F, показывает, что конечное выходное значение сети рассчитывается с использованием набора функций. Компоновка функций означает, что выходные данные одной функции используются в качестве входных данных для другой. В этом случае выходы нейронов C, D и E используются в качестве входов для нейрона F , поэтому функция, выполняемая в F , скомпонована из функций, выполняемых в C, D и E .

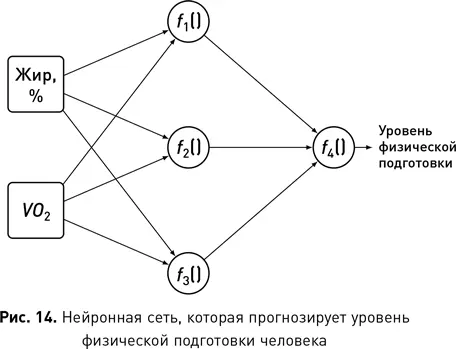
Для наглядности этого описания на рис. 14 показана нейронная сеть, которая принимает значение процентного содержания жира в организме человека и его МПК (максимальное потребление кислорода [17]) в качестве входных данных и вычисляет индивидуальный уровень физической подготовки [18]. Все нейроны в среднем слое сети вычисляют функцию на основе процентного содержания жира и МПК: f 1(), f 2() и f 3(). Каждая из этих функций моделирует взаимодействие между входами иначе, чем две другие. Эти функции по существу представляют собой новые атрибуты, которые получены сетью из необработанных входных данных. Они схожи с атрибутом ИМТ, описанным ранее, который был рассчитан как функция веса и роста. Иногда оказывается возможным интерпретировать выходные данные нейрона внутри сети, насколько это позволяет предметная область, и понять, почему этот производный атрибут полезен для сети. Однако чаще производный атрибут, рассчитанный нейроном, не будет нести никакого смысла для человека. Просто эти атрибуты фиксируют взаимодействия между другими атрибутами, которые сеть сочла полезными. Последний узел в сети f 4вычисляет другую функцию — скомпонованную из f 1(), f 2() и f 3(), — на выходе которой получается прогноз уровня физической подготовки, возвращаемый сетью. Опять же, эта функция не может быть значимой для человека, кроме того факта, что она определяет взаимодействие, которое, как обнаружила сеть, имеет высокую корреляцию с целевым атрибутом.

Обучение нейронной сети включает в себя поиск правильных весов для ее связей. Чтобы понять, как обучается сеть, полезно начать с размышлений о том, как отдельный нейрон обучается рассчитывать вес связи. Предположим, что у нас есть обучающий набор данных, который имеет для каждого объекта и входные значения, и целевой атрибут. Также предположим, что входящим связям нейрона уже назначены веса. Если мы возьмем объект из набора данных и представим нейрону значения входных атрибутов этого объекта, он выдаст прогноз для цели. Вычитая этот прогноз из значения целевого атрибута в наборе данных, мы сможем измерить отклонение нейрона для этого объекта. Используя ряд простых вычислений, можно вывести правило для обновления весов входящих связей нейрона с учетом выходного отклонения нейрона, чтобы уменьшить выходное отклонение. Точное определение этого правила будет варьироваться в зависимости от функции активации, используемой нейроном, поскольку она влияет на производную, используемую при выводе правила. Но можно дать следующее наглядное пояснение того, как работает правило обновления веса:

1. Если отклонение равно 0, не меняйте веса на входах.

2. Если отклонение положительное, требуется увеличить прогнозное значение, поэтому нужно прибавить веса всех связей с положительным входом и понизить веса связей с отрицательным.

3. Если отклонение отрицательное, требуется уменьшить прогнозное значение, поэтому нужно понизить веса всех связей с положительным входом и прибавить веса связей с отрицательным.

Сложность обучения нейронной сети состоит в том, что правило обновления веса требует оценки ошибки в нейроне, и, хотя вычислить ошибку для каждого нейрона в выходном слое сети довольно просто, сделать то же самое для нейронов в более ранних слоях намного сложнее. Стандартный способ обучения нейронной сети заключается в использовании алгоритма, называемого методом обратного распространения ошибки. Алгоритм обратного распространения является алгоритмом машинного обучения с учителем, поэтому он предполагает набор обучающих данных, который бы имел как входные значения, так и целевой атрибут для каждого объекта. Обучение начинается с назначения случайных весов каждой связи в сети. Затем алгоритм итеративно обновляет весовые коэффициенты, показывая сети обучающие объекты из набора данных и обновляя весовые коэффициенты до тех пор, пока сеть не начнет работать как ожидалось. Алгоритму присваивается имя, потому что после того, как каждый обучающий объект представлен сети, ее веса обновляются путем последовательных шагов в направлении назад по сети: