Джон Келлехер - Наука о данных. Базовый курс

В регрессионном анализе параметры функции регрессии изначально неизвестны. Установка этих параметров эквивалентна поиску строки, которая наилучшим образом соответствует данным. Стратегия установки этих параметров состоит в том, чтобы начать со случайных значений, а затем итеративно обновлять параметры, уменьшая общее отклонение функции в наборе данных. Общее отклонение рассчитывается в три этапа:

1. Функция применяется к набору данных и для каждого объекта в наборе оценивает значение целевого атрибута.

2. Отклонение функции для каждого объекта вычисляется путем вычитания оценочного значения целевого атрибута из его фактического значения.

3. Отклонение функции для каждого объекта возводится в квадрат, а затем эти возведенные в квадрат значения суммируются.

Отклонение функции для каждого объекта возводится в квадрат на последнем шаге так, чтобы отклонение, когда функция завышает значение, не отменялось отклонением, когда цель недооценена. Возведение в квадрат и в том и в другом случае придает отклонению положительное значение. Этот параметр известен как сумма квадратов отклонений , а стратегия подбора линейной функции путем поиска параметров, минимизирующих сумму квадратов отклонений (SSE), называется методом наименьших квадратов. SSE определяется как

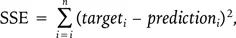
где набор данных содержит n объектов, targeti — это значение целевого атрибута для объекта i в наборе данных, а predictioni — оценка функцией цели для того же объекта.

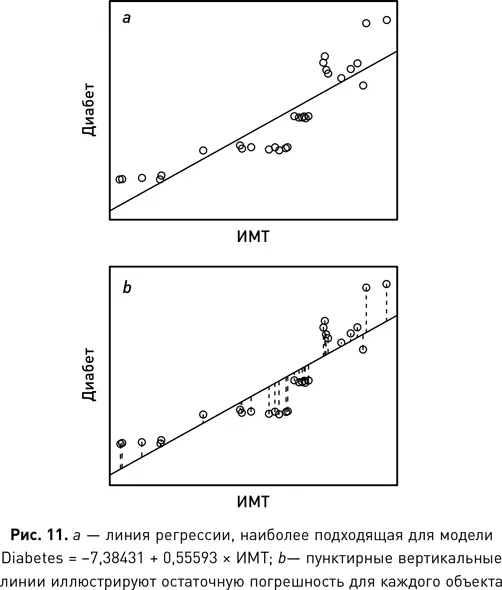
Чтобы создать линейную регрессионную модель прогнозирования, которая оценивает вероятность развития диабета у человека с учетом его ИМТ, мы заменяем Х на атрибут ИМТ, а Y — на атрибут «Диабет» и применяем алгоритм наименьших квадратов, чтобы найти наиболее подходящую прямую для этого набора данных. Рис. 11 a иллюстрирует эту прямую и ее расположение относительно объектов в наборе данных. На рис. 11 b пунктирными линиями показано отклонение (или остаток) для каждого объекта в этой прямой. При использовании метода наименьших квадратов линией наилучшего соответствия будет прямая, которая минимизирует сумму квадратов отклонений. Вот уравнение для этой прямой:

Диабет = −7,38431 + 0,55593 × ИМТ.

Значение угла наклона прямой = 0,55593 указывает на то, что для каждого увеличения ИМТ на 1 единицу модель увеличивает предполагаемую вероятность развития диабета у человека чуть более чем на 0,5 %. Чтобы предсказать вероятность развития диабета у человека, мы просто вводим его значение ИМТ в модель. Например, когда ИМТ = 20, модель возвращает прогноз 3,73 % для атрибута «Диабет», а для ИМТ = 21 модель прогнозирует 4,29 % вероятности [15].

Линейная регрессия, использующая метод наименьших квадратов, рассчитывает средневзвешенное значение для объектов. Фактически значение сдвига линии по вертикали ω 0 = −7,38431 гарантирует, что линия наилучшего соответствия проходит точку, определенную средним значением ИМТ и средним значением диабета для набора данных. Если ввести среднее значение ИМТ в наборе данных (ИМТ = 24,0932), модель оценивает атрибут диабета как 4,29 %, что является средним значением для всего набора данных.

Взвешивание объектов основано на их расстоянии от линии — чем дальше объект находится от линии, тем его отклонение выше и алгоритм будет взвешивать экземпляр по квадрату этого отклонения. Как следствие, объекты, которые имеют экстремальные значения (выбросы), могут оказать непропорционально большое влияние на процесс вычерчивания линии, в результате чего она будет удалена от других объектов. Поэтому перед использованием метода наименьших квадратов важно проверить наличие выбросов в наборе данных.

Модели линейной регрессии могут быть расширены, чтобы принимать несколько входных значений. Новый параметр добавляется в модель для каждого нового входного атрибута, а уравнение обновляется, чтобы суммировать результат умножения нового атрибута. Например, чтобы расширить модель для включения в нее в качестве входных данных атрибутов веса и времени, затраченного на физические упражнения, структура функции регрессии станет такой:

Диабет = ω 0 + ω 1ИМТ + ω 2Упражнения + ω 3Вес.

В статистике функция регрессии, которая прогнозирует переменную на основе нескольких факторов, называется функцией множественной линейной регрессии. Структура функции такой регрессии является основой для ряда алгоритмов машинного обучения, включая и нейронные сети.

Между корреляцией и регрессией наблюдаются сходства, поскольку и та и другая представляют собой техники, сосредоточенные на выявлении зависимостей между столбцами в наборе данных. Корреляция ищет взаимосвязь между двумя атрибутами, а регрессия сосредоточена на прогнозировании значений зависимой переменной при нескольких входных атрибутах. В частных случаях коэффициент корреляции Пирсона измеряет степень линейной зависимости двух атрибутов, а линейная регрессия, обученная по методу наименьших квадратов, представляет собой процесс поиска линии наилучшего соответствия, которая прогнозирует значение одного атрибута при заданном значении другого.

Нейронная сеть состоит из нейронов, соединенных друг с другом. Нейрон принимает набор числовых значений в качестве входных данных и сопоставляет их с одним выходным значением. По своей сути нейрон — это функция линейной регрессии с несколькими входами. Единственное существенное различие состоит в том, что в нейроне выходной сигнал определяется другой функцией, которая называется функцией активации.

Функции активации, как правило, отображают выходной сигнал множественной линейной регрессии нелинейно. В качестве функций активации наиболее часто применяются логистическая функция и функция tanh (рис. 12). Обе функции принимают на вход одно значение x , являющееся выходным значением функции множественной линейной регрессии, которую нейрон применяет к своим входным данным. Также обе функции используют число Эйлера, приблизительно равное 2,71828182. Эти функции иногда называют функциями сжатия, поскольку они принимают любое значение от «плюс бесконечности» до «минус бесконечности» и отображают его в небольшом заранее определенном диапазоне. Диапазон выходных значений логистической функции составляет от 0 до 1, а функции tanh — от –1 до 1. Следовательно, выходные значения нейрона, который использует логистическую функцию в качестве своей функции активации, всегда находятся в диапазоне от 0 до 1. Тот факт, что обе функция используют нелинейные отображения, ясно по S-образной форме кривых. Причиной введения нелинейного отображения в нейрон является то, что одним из ограничений функции линейной регрессии с несколькими входами является ее линейность по определению, и если все нейроны в сети будут выполнять только линейные отображения, то и сама сеть также будет ограничена изучением линейных функций. Однако нелинейная функция активации в нейронах сети позволяет ей изучать более сложные (нелинейные) функции.