Миран Липовача - Изучай Haskell во имя добра!

А что у нас с операцией >>=? Выглядит несколько мудрёно, поэтому давайте воспользуемся тем, что для монад выражение m >>= fвсегда равно выражению join (fmap f m), и подумаем, как бы мы разгладили список вероятностей списков вероятностей. В качестве примера рассмотрим список, где существует 25-процентный шанс, что случится именно 'a'или 'b'. И 'a', и 'b'могут появиться с равной вероятностью. Также есть шанс 75%, что случится именно 'c'или 'd'. То есть 'c'и 'd'также могут появиться с равной вероятностью. Вот рисунок списка вероятностей, который моделирует данный сценарий:

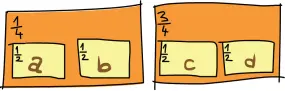
Каковы шансы появления каждой из этих букв? Если бы мы должны были изобразить просто четыре коробки, каждая из которых содержит вероятность, какими были бы эти вероятности? Чтобы узнать это, достаточно умножить каждую вероятность на все вероятности, которые в ней содержатся. Значение 'a'появилось бы один раз из восьми, как и 'b', потому что если мы умножим одну четвёртую на одну четвёртую, то получим одну восьмую. Значение 'c'появилось бы три раза из восьми, потому что три четвёртых, умноженные на одну вторую, – это три восьмых. Значение 'd'также появилось бы три раза из восьми. Если мы сложим все вероятности, они по-прежнему будут давать в сумме единицу.

Вот эта ситуация, выраженная в форме списка вероятностей:

thisSituation :: Prob (Prob Char)

thisSituation = Prob

[(Prob [('a',1 % 2),('b',1 % 2)], 1 % 4)

,(Prob [('c',1 % 2),('d',1 % 2)], 3 % 4)

]

Обратите внимание, её тип – Prob (Prob Char). Поэтому теперь, когда мы поняли, как разгладить вложенный список вероятностей, всё, что нам нужно сделать, – написать для этого код. Затем мы можем определить операцию >>=просто как join (fmap f m), и заполучим монаду! Итак, вот функция flatten, которую мы будем использовать, потому что имя joinуже занято:

flatten :: Prob (Prob a) –> Prob a

flatten (Prob xs) = Prob $ concat $ map multAll xs

where multAll (Prob innerxs, p) = map (\(x, r) –> (x, p*r)) innerxs

Функция multAllпринимает кортеж, состоящий из списка вероятностей и вероятности p, которая к нему приложена, а затем умножает каждую внутреннюю вероятность на p, возвращая список пар элементов и вероятностей. Мы отображаем каждую пару в нашем списке вероятностей с помощью функции multAll, а затем просто разглаживаем результирующий вложенный список.

Теперь у нас есть всё, что нам нужно. Мы можем написать экземпляр класса Monad!

instance Monad Prob where

return x = Prob [(x,1 % 1)]

m >>= f = flatten (fmap f m)

fail _ = Prob []

Поскольку мы уже сделали всю тяжелую работу, экземпляр очень прост. Мы определили функцию fail, которая такова же, как и для списков, поэтому если при сопоставлении с образцом в выражении doпроисходит неудача, неудача случается в контексте списка вероятностей.

Важно также проверить, что для только что созданной нами монады выполняются законы монад:

1. Первое правило говорит, что выражение return x >>= fдолжно равняться выражению f x. Точное доказательство было бы довольно громоздким, но нам видно, что если мы поместим значение в контекст по умолчанию с помощью функции return, затем отобразим это с помощью функции, используя fmap, а потом отобразим результирующий список вероятностей, то каждая вероятность, являющаяся результатом функции, была бы умножена на вероятность 1 % 1, которую мы создали с помощью функции return, так что это не повлияло бы на контекст.

2. Второе правило утверждает, что выражение m >> returnничем не отличается от m. Для нашего примера доказательство того, что выражение m >> returnравно просто m, аналогично доказательству первого закона.

3. Третий закон утверждает, что выражение f <=< (g <=< h)должно быть аналогично выражению (f <=< g) <=< h. Это тоже верно, потому что данное правило выполняется для списковой монады, которая составляет основу для монады вероятностей, и потому что умножение ассоциативно. 1 % 2 * (1 % 3 * 1 % 5)равно (1 % 2 * 1 % 3) * 1 % 5.

Теперь, когда у нас есть монада, что мы можем с ней делать? Она может помочь нам выполнять вычисления с вероятностями. Мы можем обрабатывать вероятностные события как значения с контекстами, а монада вероятностей обеспечит отражение этих вероятностей в вероятностях окончательного результата.

Скажем, у нас есть две обычные монеты и одна монета, с одной стороны налитая свинцом: она поразительным образом выпадает на решку девять раз из десяти и на орла – лишь один раз из десяти. Если мы подбросим все монеты одновременно, какова вероятность того, что все они выпадут на решку? Во-первых, давайте создадим значения вероятностей для подбрасывания обычной монеты и для монеты, налитой свинцом:

data Coin = Heads | Tails deriving (Show, Eq)

coin :: Prob Coin

coin = Prob [(Heads,1 % 2),(Tails,1 % 2)]

loadedCoin :: Prob Coin

loadedCoin = Prob [(Heads,1 % 10),(Tails,9 % 10)]

И наконец, действие по подбрасыванию монет:

import Data.List (all)

flipThree :: Prob Bool

flipThree = do

a <���– coin

b <���– coin

c <���– loadedCoin

return (all (==Tails) [a,b,c])

При попытке запустить его видно, что вероятность выпадения решки у всех трёх монет не так высока, даже несмотря на жульничество с нашей налитой свинцом монетой:

ghci> getProb flipThree

[(False,1 % 40),(False,9 % 40),(False,1 % 40),(False,9 % 40),

(False,1 % 40),(False,9 % 40),(False,1 % 40),(True,9 % 40)]

Все три приземлятся решкой вверх 9 раз из 40, что составляет менее 25%!.. Видно, что наша монада не знает, как соединить все исходы False, где все монеты не приземляются решкой вверх, в один исход. Впрочем, это не такая серьёзная проблема, поскольку написание функции для вставки всех одинаковых исходов в один исход довольно просто (это упражнение я оставляю вам в качестве домашнего задания).

В этом разделе мы перешли от вопроса («Что если бы списки также содержали информацию о вероятностях?») к созданию типа, распознанию монады и, наконец, созданию экземпляра и выполнению с ним некоторых действий. Думаю, это очаровательно! К этому времени у вас уже должно сложиться довольно неплохое понимание монад и их сути.

Хотя чистота языка Haskell даёт море преимуществ, вместе с тем он заставляет нас решать некоторые проблемы не так, как мы решали бы их в нечистых языках.

Из-за прозрачности ссылок одно значение в языке Haskell всё равно что другое, если оно представляет то же самое. Поэтому если у нас есть дерево, заполненное пятёрками (или, может, пятернями?), и мы хотим изменить одну из них на шестёрку, мы должны каким-то образом понимать, какую именно пятёрку в нашем дереве мы хотим изменить. Нам нужно знать, где в нашем дереве она находится. В нечистых языках можно было бы просто указать, где в памяти находится пятёрка, и изменить её. Но в языке Haskell одна пятёрка – всё равно что другая, поэтому нельзя проводить различие исходя из их расположения в памяти.