Жак Арсак - Программирование игр и головоломок

*** Игра 26.Могущественная четверка.

Эта игра продается на рынке в другой форме. Она происходит в прямоугольном пространстве с 5 строками и 7 столбцами. Игра ориентирована, у нее есть низ и верх. Игровые позиции суть наинизшие свободные места в каждом столбце. Каждый игрок на своем ходе помещает свой отличительный знак на одно из игровых полей: например, один ставит крестики (+), другой — нолики (0). Первый, кто поставит на одной линии четыре принадлежащих ему знака — либо горизонтально, либо вертикально, либо по диагонали — выигрывает. На рис. 16 будем считать, что нолики при игре ставит тот игрок, чей ход именно сейчас. Если он не сыграет немедленно в пятом столбце, то его противник выиграет следующим ходом. По диагонали, начинающейся у основания четвертого столбца и идущей влево и вверх, есть три нолика, но единственное игровое поле в первом столбце обозначено точкой, и немедленно реализовать продолжение линии поэтому нельзя. Очевидно, что его противник не имеет никакого желания служить ему подставкой при пополнении первого столбца вместо того, чтобы заниматься разыгрыванием мест, допускающих продолжение линии…

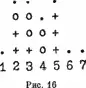
Эту игру, производную от вошек, программировать намного проще, потому что всего полей только 35, и только 7 из них являются игровыми полями на каждом ходе. Это существенно ограничивает работу. В реализованной мною версии ответ микрокомпьютера практически мгновенный (порядка секунды). Я не думаю, что я располагаю программой-чемпионом, я не очень хорошо знаком с атим родом игр…

Я объединил в этой главе несколько игр, которые можно найти на рынке и для которых существует стратегия решения. Как только она становится известной, игра теряет всякий интерес. Единственное связанное с такими играми удовольствие — обнаружить, как с ними покончить. Поэтому напишите программу — это наилучший способ сформулировать выигрышную стратегию, а затем забудьте игру, она вам больше ничего не принесет. И тем хуже, если продавцы этих игр не согласятся со мной… Некоторые из этих игр являются классическими среди информатиков. Я попытался их немного подновить. Многие стратегии могут быть элегантно запрограммированы с помощью рекурсивных процедур, но на языке Бейсик это невозможно. Всегда наступает день, когда фанатики этого языка, такого удобного для первых шагов, начинают понимать его ограниченность… Рекурсивность допустима в языках LSE и Паскаль.

? Игра 27.Бездельник.

Эта игра на рынке есть. Она имеет вид дощечки, в которую продето n гвоздей, скользящих через соответствующее отверстие, причем концы гвоздей расплющены и в каждом просверлено отверстие, в которое продето кольцо. Вы безусловно можете изготовить все это сами, используя достаточно толстые гвозди (диаметром порядка четырех миллиметров). Пропустите гвоздь в отверстие в 5 миллиметров в дощечке, а затем расплющите острие молотком. Просверлите головку наконечника, образовавшуюся у конца гвоздя, и вставьте туда кольцо для ключей. Каждое кольцо должно проходить вокруг предыдущего гвоздя. Трудность игры зависит от n . Для n = 6 она довольно быстро приходит к концу. Для n = 8 она требуем долгих минут. Она почти невыполнима, если n больше восьми.

Через кольца проходит челнок, длинный замкнутый контур, представленный на рисунке. Дело в том, чтобы его вынуть и, таким образом, освободить от колец (рис. 17).

Первое, что нужно сделать — это научиться, как пропускать одно кольцо через челнок, или как его оттуда вынуть. Несколько манипуляций — и вы быстро убеждаетесь, что в какой стадии ни была бы игра, всегда можно надеть или снять первое кольцо, которое свободно (не проходит вокруг какого-либо гвоздя). Можно также освободить кольцо, которое следует за первым занятым кольцом (если оно проходит вокруг челнока), или одеть его на челнок, если оно не одето. Таким образом, игру «бездельник» можно заменить равносильной игрой, которую легче представить на компьютере.

Эта игра ведется на таблице, разделенной на несколько полей (8 полей на рисунке). В начальном состоянии каждое поле покрыто шашкой. Поля размечены цифрами. Играть на данном поле — значит, поставить туда шашку, если поле пусто, и удалить шашку, стоящую на этом поле — в противоположном случае. Правила игры следующие:

— можно всегда играть на первом поле,

— можно играть на поле, которое следует за первым занятым полем.

Есть две возможных игры:

НАДЕВАТЬ: игровое поле вначале пусто. Заполнить все поля.

СНИМАТЬ: игровое поле вначале наполнено шашками на каждой клетке. Нужно все убрать,

Эта задача имеет очень элегантное рекурсивное решение. Но если вы немного подумаете, то вы сможете также найти очень простое итеративное решение, причем игра НАДЕВАТЬ оказывается более простой, чем игра СНИМАТЬ.

Вот другая интерпретация этой игры — для тех, кто любит арифметику. Вы можете считать, что каждое поле может принимать два состояния (свободное и занятое), что эквивалентно двоичным числам — например, 0 для свободного и 1 для занятого полей. Тогда каждая конфигурация является представлением целого числа по основанию 2. Таким образом, рис. 18 представляет целое число 11111111 в качестве начального состояния и 01011011 в качестве промежуточного состояния. Ниже нам будет удобно читать эти слова в обратном порядке, так что в этих новых обозначениях промежуточное состояние соответствует двоичному числу 11011010.

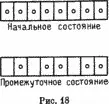
Ясно, что эта игра порождает последовательность чисел (в приведенном выше примере число равно 218 в десятичной записи). При переходе от одного числа к следующему меняется лишь одна двоичная цифра. Можете ли вы сказать, какая последовательность порождается таким образом в каждой из игр?

?* Игра 28.Зануда,

Эта игра называется также «игра в лягушек». У нее была версия, использованная в материалах лицеев, но в ней было не все, что я вам сейчас предлагаю. Игровое поле снова имеет вид прямоугольной площадки, разделенной на поля. Число полей должно быть нечетным (9 на рис. 19). Поля слева покрыты шашками некоторого цвета (я представил их ноликами), поля справа — шашками другого цвета (здесь — крестиками). Среднее поле свободно. Крестики могут передвигаться только влево, нолики — только вправо. Шашка может быть либо подвинута на один шаг, если следующее поле в направлении ее перемещения свободно, либо перепрыгнуть через шашку другого рода, если следующее за ней поле свободно. Рисунок 20 иллюстрирует два возможных хода в партии с начальным положением на рис. 19.