Жак Арсак - Программирование игр и головоломок

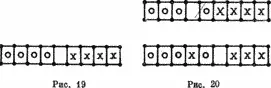
Цель игры состоит в том, чтобы привести все X влево, а все 0 вправо, так что конечное состояние должно быть похоже на начальное, и шашки должны поменяться местами (крестики справа, нолики слева).

Программа, которую вы должны составить, должна описывать последовательность перемещений шашек для произвольного (но, конечно, нечетного) числа полей. Вы можете получить решение в виде пары рекурсивных процедур или в виде одной итеративной программы. Как только вы найдёте стратегию, зануда не будет больше представлять никакого интереса. Как это случилось с теми, с кем я занимался на Митра 15, в лицее, требуя, чтобы игрок сидел за своей клавиатурой и переставлял шашки. Но если не знать стратегии и действовать случайным образом, то выиграть нельзя вследствие теоремы Дюнойе: «Если какой-то выбор вы делаете случайным образом, то вы всегда проигрываете». Это нам постоянно повторял наш учитель математики, когда я был в подготовительном классе Политехнической школы. Мы придумали следствие: поскольку мы всегда проигрываем при случайном выборе, то достаточно после этого выбора выбрать другую сторону альтернативы. Но это дает выход из парадокса Дюнойе (я совершенно не знаю, кто такой Дюнойе. Это — существенный момент истории науки, который следовало бы прояснить. Всегда цитируют Мэрфи и его знаменитые законы: если в некотором опыте что-то может разладиться, то можно быть уверенным, что это обязательно произойдет. Если, кроме того, при этом в комнате есть посторонний наблюдатель, то он прибавит «ну, я же так и говорил…». Дюнойе — предшественник Мэрфи), Вот в чем парадокс. Есть альтернатива. Вы выбрали случайным образом и обманулись. Следовательно, если вы взяли другую сторону альтернативы, то вы оказались правы. Но это — тоже случайный выбор, поэтому вы опять обманулись…

?* Игра 29.Б — А — БА.

Эта игра вовсе не потому самая простая среди всех игр этого сорта, что она называется б—а—ба. Согласно [BAL], она имеет японское происхождение. Ее можно сформулировать следующим образом. Игра разыгрывается на площадке, разделенной на клетки, на этот раз в четном числе. Есть шашки двух сортов, скажем, крестики и нолики — как в «зануде». В начале игры два левых поля свободны, остальные заняты поочередно 0 и X, как указано на рис. 21. При каждом ходе вы можете переместить пару смежных шашек, перенося ее на пару смежных свободных клеток. Вы выиграете, когда все X будут вместе стоять на левых полях, затем будут нолики, а два правых поля останутся свободными.

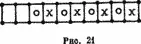
Можно также представить это другим способом. Свободные поля представляются точками (рис. 22), остальные заняты буквами а и б (вот вам и б — а — ба ).

Пара шашек, которая переносится при данном ходе, абсолютно произвольна: две одинаковых буквы, две разных буквы, все равно в каком порядке…

Начните с решения задачи для 8 букв и 10 полей, как на рисунке. Это очень просто и у вас нет необходимости » компьютере. Попробуйте затем решить ее для бо́льшего числа полей.

Честно говоря, я соответствующую программу не написал, потому что ее использование на компьютере меня ничему новому не научило бы. То, что здесь приведено, подходит программисту, который на что-то рассчитывает. Если у вас есть склонность к программированию, то вы найдете способ решить задачу для всех случаев,

* Игра 30.Отшельник.

Может быть, мне и не следовало бы помещать «Отшельника» в эту главу, Классификация игр полностью основана на оттенках и на индивидуальных оценках. Я провел немало времени в забавах с «Отшельником», но все же верно, что едва только удается обнаружить хорошую стратегию, как интерес уменьшается. Возможность его программирования связана с улучшениями. «Отшельник» разыгрывается на площадке с проделанными в ней отверстиями, в которых могут быть размещены шашки. Но можно также использовать доску, на которой нарисованы поля, а можно также все это очень хорошо нарисовать на земле и использовать камешки в качестве шашек — точно так же, как я рассказывал при игре в лис и кур. Впрочем, может оказаться, что «отшельник» был изобретен каким-нибудь знатным французом, заключенным в Бастилию, который модифицировал игру в лиси кур.

Рисунок 23 представляет одно из состояний игры в «Отшельника». Свободные места представлены точками, шашки — знаком ×. Как показывает название, это — игра для одного-единственного лица. При каждом ходе нужно съесть шашку, заставляя перепрыгнуть через нее другую шашку так, чтобы попасть на свободное поле — либо горизонтально, либо вертикально. Так, на рис. 23 имеется 4 возможных хода:

— шашка, лежащая на пересечении планок креста, может ваять шашку, расположенную непосредственно над ней, и попасть в середину верхней строки (шашка, через которую перепрыгнули, а именно, расположенная в вершине креста, удаляется из игры);

— та же шашка может взять шашку слева;

— или шашку справа;

— наконец, шашка в центре игрового поля может взять шашку под ней, расположенную в низу креста.

Цель игры состоит в том, чтобы удалить все шашки, кроме одной. Число необходимых для этого ходов легко подсчитать: поскольку при каждом ходе берется одна шашка, то число ходов равно числу подлежащих удалению шашек. В случае креста на рис. 23 вам осталось сделать до конца еще 5 ходов.

Составьте программу для отшельника. Вы даете компьютеру начальную конфигурацию, например крест на рис. 23. Он сообщает вам ходы, которые приводят к решению.

Другие конфигурации приведены на рис. 24.

В своей наиболее общей форме эта игра начинается с игрового доля, полностью покрытого шашками, кроме единственного остающегося свободным поля. Попробуйте заставить вашу программу работать и в этом случае. У вас появится новая трудность, связанная с симметрией игры: есть много решений, эквивалентных с точностью до симметрии.

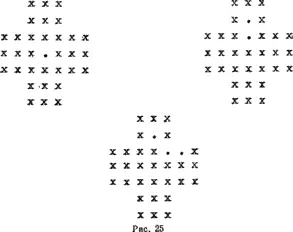
На рис. 25 сначала изображена исходная конфигурация. Есть 4 различных хода — шашка из перекладины креста прыгает в центр игрового поля. Эти 4 хода начинают 4 решения, эквивалентных с точностью до поворота на прямые углы. После этого остаются еще две возможности эквивалентности с помощью симметрии относительно вертикальной оси игры. Нижняя конфигурация показывает результат одного из этих ходов.